
"CQ-SKW", №16, август, 1930 год, стр. 130-132

инж. З. Гинзбург
Сечение сердечника стержня может быть получено также приближенно из следующей формулы:
Зная ширину железа g в том месте, где на него должна быть надета катушка, легко можно высчитать толщину сердечника
| b = | Q | см (2) |
| g · 0,85 |
Величина 0,85 представляет собой коэффициент заполнения сечения железом.
Число листов железа, необходимых для получения нужного сечения Q, найдем из формулы
| n = | Q | (3) |
| g · p |
где р — толщина железа в мм.
Работа катушки самоиндукции, внутри которой имеется железный сердечник, будет зависеть от того, насколько последний намагничен, т. е. какой магнитной проницаемостью обладает в данный момент железо, его составляющее.
Как известно, самоиндукция увеличивается с увеличением магнитной проницаемости сердечника. Создавая условия изменяющие величину µ, мы тем самым будем изменять самоиндукцию дросселя.
Нетрудно сообразить, что магнитная проницаемость в свою очередь связана с той силой тока, которая протекает через дроссель. Ведь с увеличением тока увеличится магнитный поток, который проходит по железному сердечнику, а он вызовет увеличение магнитной индукции В и соответственное изменение µ.
Таким образом мы видим, что между самоиндукцией дросселя, его данными, силой тока, магнитной проницаемостью и магнитной индукцией существует определенное численное соотношение. Пользуясь этим соотношением и имея некоторые заданные величины, как то: самоиндукцию, нормальную силу тока дросселя, сечение его сердечника и магнитную индукцию, мы сможем определить то число витков, которое должен иметь дроссель при выбранном нами токе («нормальном») для получения желаемой самоиндукции.
Определяется оно по формуле:
| W = | LJн | 108 (4) |
| QB |
В этой формуле: W — число витков, В — магнитная индукция, т. е. число силовых линий магнитного потока, приходящегося на 1 кв. см сечения сердечника. Для обыкновенного железа среднего качества величина В берется от 6 000 до 8 000 силовых линий на кв. см. В случае применения специальных сортов железа величина В берется соответствующей этому сорту железа.
Допуская в обмотке катушки плотность тока в 1 ампер на кв. мм сечения провода, найдем это сечение.
| q = | J | (5) |
| 1 |
откуда диаметр расчетный будет
По полученным данным можно строить и собирать дроссель, так как размеры и данные нами определены.
Для установки дросселя на работу остается еще подсчитать величину воздушного зазора между частями магнитопровода.
Дроссель будет хорошо работать лишь при том условии, когда образующийся в сердечнике магнитный поток Ф будет изменяться пропорционально силе тока. Это имеет место, когда железо не достигает насыщения, так как вблизи насыщения пропорциональность между током и магнитным потоком нарушается. Воздушный зазор позволяет регулировать величину магнитного потока и подбирать его так, чтобы не доводить до насыщения железа сердечника.
Если режим работы передатчика будет всегда одинаковым и сила анодного тока не будет нами изменяться, то для такого нормального тока мы можем подсчитать величину воздушного зазора упрощенным способом, пользуясь для этого нижеследующей приближенной формулой
| lвозд. = | 4πW2 · Q | · 10—9 (7) |
| L |
где l — общая длина воздушного разора в см (в магнитопроводе дросселя имеется два зазора), W — число витков дросселя, Q — сечение стержня.
Рассчитанный таким образом зазор не всегда может оказаться вполне удовлетворительным, так как отношение длины зазора к длине того железного пути, по которому проходит магнитный поток, должно быть заключено в известном пределе. При малом значении этого отношения может наступить быстрое насыщение даже при небольшом увеличении тока; большое же значение ведет к большому рассеиванию магнитного потока, что в свою очередь вызывает понижение самоиндукции против расчетной величины.
Согласно опыту, величина этого соотношения должна находиться в пределах:
| 0,003 | < | lвозд. | < | 0,025 (8) |
| lжел. |
Следует однако сказать, что в том случае, когда дроссель должен служить для работы при разных токах, отличающихся по своей величине от нормального, такой упрощенный подсчет зазора оказывается непригодным, потому что с изменением силы тока, во избежание насыщения железа, приходится также изменять и величину воздушного зазора. Приходится воздушный зазор подсчитывать для целого ряда токов, отличающихся от нормального, в пределах от 50 до 150% от него.
Этот способ хотя и более сложен и кропотлив, но зато более точен и позволяет рационально использовать дроссель при самых разнообразных нагрузках.
Подсчет делается для нескольких токов, как превышающих нормальный, так и меньших последнего. Берутся, например, силы тока в 50, 75, 100, 125, 150% и т. д., для каждого из них высчитывается нужный зазор и затем по полученным данным строится кривая, дающая зависимость между силой тока и воздушным зазором. Пользование такой кривой позволяет легко и быстро определять во время работы воздушный промежуток дросселя и моментально производить его «настройку».
Здесь кстати будет сказать, как практически делается воздушный промежуток и как он изменяется. Обычно принято думать, что зазор должен быть действительно воздушным, а накладка (якорь) как бы подвешивается на известном расстоянии над основным сердечником. Такое мнение совершенно не обосновано и приводит лишь к ряду конструктивных трудностей. В действительности в зазорах вместо воздуха помещаются прокладки нужной толщины. Делаются они из дерева, картона, фибры и т. п. немагнитных веществ. Таким образом изменение величины зазора сводится только к увеличению или уменьшению числа и толщины прокладок, что может быть выполнено достаточно быстро.
Переходим к расчету.
Полное число ампер-витков дросселя выразится произведением числа витков на силу тока в амперах.
Ампер-витки определяют магнитодвижущую силу, которая расходуется на преодоление магнитного сопротивления всей магнитной цепи в целом. Магнитная цепь состоит (рис. 6) из основного сердечника со средней длиной магнитного пути l1, из двух воздушных зазоров, каждый длиной ½lвозд., и накладки—якоря со средней длиной l2. Средние длины показаны на рисунке пунктирной линией.

Тогда магнитодвижущая сила разделится на две части, из коих одна пойдет на преодоление магнитного сопротивления в железе на длине lж = l1 + l2, а другая — на преодоление того же сопротивления в воздухе, т. е. на длине lвозд..
Определим первую часть.
Если на намагничивание одного погонного сантиметра магнитного пути в железе понадобится awж ампер витков, то на lж сантиметров их понадобится в lж раз больше. Отсюда
Число ампер витков на один погонный сантиметр awж зависит от магнитной индукции и может быть взято из следующей таблицы для среднего железа, зная магнитную индукцию В:
| Магнитная индукция В |
Ампервитки на 1 см — awж |
Магнитная индукция В |
Ампервитки на 1 см — awж |
| 1 000 | 0,46 | 9 000 | 1,58 |
| 2 000 | 0,57 | 10 000 | 1,80 |
| 3 000 | 0,65 | 11 000 | 2,37 |
| 4 000 | 0,75 | 12 000 | 3,20 |
| 5 000 | 0,85 | 13 000 | 4,50 |
| 6 000 | 1,00 | 14 000 | 6,50 |
| 7 000 | 1,16 | 15 000 | 10,90 |
| 8 000 | 1,35 | 16 000 | 20,0 |
| 17 000 | 42,0 |
Число ампер витков, расходуемых на намагничивание воздушного промежутка, определится как разность между общим числом ампер витков и полученным по формуле (10):
Отсюда находим общую длину воздушного пути:
| lвозд. = | 0,4 · π · (AW)в | см (12) |
| B |
Так как воздушных зазоров два, то каждый из них будет равен половние lвозд..
Полученный результат (12) проверяем по выражению (8).
Подобный расчет воздушного зазора, как уже было сказано выше, делается для нескольких значений силы тока; результаты сводятся в таблицу такой формы:
| Сила тока J амп. |
% от нор- мального тока |
Воздушный зазор l ½ |
Падение на- пряжения в дросселе |
по которой строятся кривые.
Последняя величина, именно падение напряжения в дросселе, берется по формуле
| e = J · | w · l0 | вольт |
| 57 · q |
w — число витков, l0 — средняя длина одного витка провода в метрах, q — сечение провода в кв. мм; e — падение напряжения в дросселе в вольтах (легко сообразить, что W·l0/57q есть примерное омическое сопротивление дросселя).
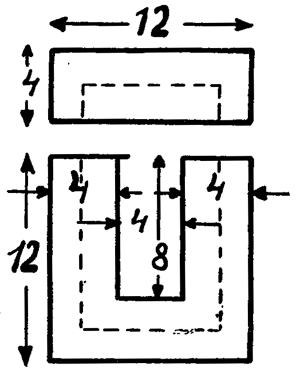
Для примера сделаем расчет дросселя на 50 генри для тока в 100 — МА — 0,1 амп. для железа, показанного на рис. 7.
Сперва по формуле (1) вычисляем А:
По кривой рис. 5 для значения 500 (так как на кривой обозначения для LI2 даны в тысячных долях) находим для сердечника с отношением 2 сечение Q = 8 кв. см.
Для проверки можно вычислять Q по формуле (1-а)
Разница таким образом получается небольшая. При сечении сердечника в 8 кв. см и при ширине его g — 4 см толщина (по формуле 2) будет:
| b = | 8 | ≈ 2,4 см |
| 4 · 0,85 |
Число листов железа при толщине листа в 0,2 мм
| n = | 8 | = 100 шт. |
| 4 · 0,02 |
Число витков получим по формуле 4, считая В = 7000
| w = | 50 · 0,1 | 108 ≈ 8 930 витков. |
| 8 · 7 000 |
Сечение провода при нормальном токе в 100 ма.
| q = | 0,1 | = 0,1 кв. мм. |
| 1 |
Диаметр провода по формуле 6
Для осуществления намотки выбираем ближайший размер из существующих, именно 0,35 мм.
Теперь переходим в расчету воздушного зазора. Расчет сделан одновременно для трех значений тока 50, 100 и 150% от нормального, т. е. для 50, 100 и 150 миллиампер.
Полное число ампер витков вычисляется по формуле 9.
Длина среднего пути магнитного потока в железе
Беря по таблице для В = 7 000, awж = 1,16, находим число ампер витков, идущих на намагничивание железа для всех трех токов:
Тогда число ампервитков для воздушного зазора будет;
Откуда длина воздушных промежутков
| Iв = | 0,4 · 3,14 · 400,1 | = 0,072 см; |
| 7 000 | ||
| Iв = | 0,4 · 3,14 · 846,6 | = 0,152 см; |
| 7 000 | ||
| Iв = | 0,4 · 3,14 · 1340 | = 0,241 см; |
| 7 000 |
Каждый из воздушных зазоров в этих трех случаях должен иметь размер:
1) lв : 2 = 0,36 мм. 2) lв : 2 = 0,76 мм 3) lв : 2 = 1,20 мм.
Подсчитаем омическое сопротивление катушек. Считая, что на дросселе имеется 2 по 4 465 витков, нетрудно определить среднюю длину одного витка провода; она будет l0 = 6 + 4,5 + 6 + 4,5 = 21 см =0,21 мт.
Омическое сопротивление обеих катушек
| R = | 2 · 4 465 · 0,21 | ≈ 330 ом |
| 57 · 0,1 |
Падение напряжения будет е = I · R.
1) е = 0,05 · 330 = 16,5 v. 2) е = 0,1 · 330 = 33 v и 3) e = 0,15 · 330 = 49,5 v.
По полученным результатам строим кривые для воздушного зазора и падения напряжения (рис. 8).
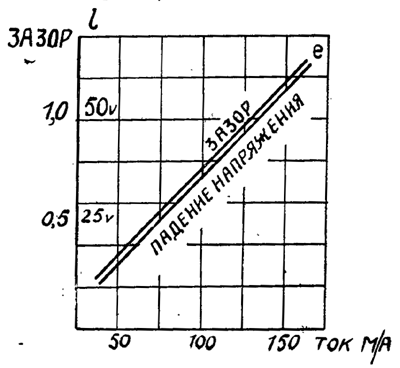
По этим кривым легко определяется длина воздушного зазора для различных других значений силы токов н соответствующие этим токам падения напряжений в дросселе.