
"Радиофронт", №33-34, ноябрь-декабрь, 1930 год, стр. 688-689

Мы уже указывали, что значение неизвестного, при котором равенство справедливо, наз. корнем уравнения. Следовательно решение уравнения сводится к отысканию его корней.
Из сказанного в прошлый раз можно вывести следующее правило: для того, чтобы решить уравнение, нужно неизвестные члены уравнения перенести в одну сторону, а известные в другую. При перенесении членов уравнения из одной части в другую знаки у них нужно переменить на обратные.
Пример:
| 21х — 3 = 7 + Х |
| 21х — Х = 7 + 3 |
| 20х = 10. |
| 20х | = | 10 | ; X = | 1 | = 0,5 |
| 20 | 20 | 2 |
Таким образом уравнение решено. После того, как корень уравнения найден, надо подставить его в уравнение, взамен неизвестного и посмотреть справедливо ли равенство. В том случае, когда при такой замене равенство справедливо — корень найден правильно.
Подставляем значение корня в уравнение:
| 21 · 0,5 — 3 = 7 + 0,5; 7,5 = 7,5. |
Корень найден правильно.
Решим уравнение:
| 1)31у — 21 = 9 + у |
| 31у — у = 9 + 21; 30у = 30; у = 1. |
Делаем проверку:
| 31 · 1 — 21 = 9 + 1; 10 = 10. |
Корень определен правильно.
| 2) 7(х + 1) = 4х — 11 |
| 7х + 7 = 4х — 11; 7х — 4х = —11 — 7 |
| 3x = —18; Х=—6. |
Проверяем:
| 7(—6 + 1) = 4(—6) — 11; |
| —35 = —24 — 11; —35 = —35. |
Корень найден правильно.
Разобрав решение уравнений, попробуем применить наши знания для решения следующей задачи: имеется формула для определения емкости слюдяного конденсатора:
| C = | 6S(n — 1) | , |
| 12,5d |
где С — емкость слюдяного конденсатора в сантиметрах, S — полезная площадь пластин, n — число пластин и d — толщина диэлектрика в сантиметрах.
В этой формуле С является тем неизвестным, которое мы определяем.
Имея эту формулу, нам нужно определить число пластин n, если известны все остальные данные конденсатора: С, S и d. То есть n является теперь тем неизвестным, которое нам надо найти.
Для этого разделим обе части формулы на
| 6S |
| 12,5d |
тогда имеем:
| 12,5dC | = n — 1; | 12,5dC | + 1 = n. |
| 6S | 6S |
В этом и заключается решение уравнения относительно n, ибо мы преобразовали формулу так, что по ней можно непосредственно определить число пластин n.
С такими преобразованиями чрезвычайно часто приходится иметь дело при вычислениях.
Часть математики, занимающаяся операциями над направленными величинами, носит название векторного исчисления.
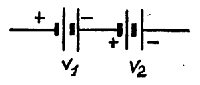
Вектором называется величина, определяющаяся численным значением и имеющая направление. (Например, сила, скорость и т. д.) Вектор изображается при помощи направленного отрезка.
Для того, чтобы отчетливо представить себе явления, происходящие в электрических цепях, очень удобно изображать напряжение и силу тока помощью векторов, т. е. отрезков, имеющих направление.
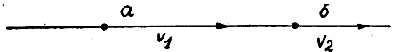
Ниже мы приведем сложение и вычитание векторов для разных случаев, встречающихся в практике. У нас имеются 2 батареи, соединенных последовательно (рис. 1). Напряжение одной батареи V1 = 5 в., а второй батареи V2 = 3 в. Надо найти общее напряжение V.
| V = V1 + V2; V = 8 в. |
Теперь решим эту задачу помощью векторов. Возьмем прямую линию и на ней в масштабе нанесем величины отрезков, соответствующие V2 и V1 (рис. 2). Оба этих вектора будут иметь одинаковое направление, так как электродвижущие силы батарей направлены в одну сторону. От точки а в масштабе отложим отрезок, соответствующий напряжению батареи V1. Пусть один вольт у нас будет равен 1 см, тогда отрезок, соответствующий V1, будет равен 5 см. От какой-либо точки в отложим отрезок, соответствующий напряжению батареи V2. Этот отрезок будет равен 3 см, так как V2 = 3 в. Направление он будет иметь то же самое, что и отрезок V1. Для того, чтобы найти общее напряжение, нужно найти сумму этих отрезков. Отрезок V2 переносим по прямой так, чтобы его конец совпал с началом отрезка V1 (рис. 3).
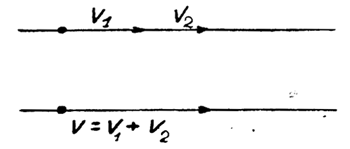
Совершенно ясно, что в этом случае напряжения батарей складываются и общее напряжение
| V = V1 + V2 = 8 вольт. |
Два таких вектора могут быть заменены одним вектором V равным V1 + V2.
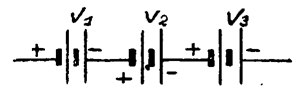
Теперь найдем общее напряжение 3 батарей, соединенных последовательно (рис. 4).
| V1 = 2 в.; V2 = 4 в.; V3 = 1 в. |
Общее напряжение V
| V = V1 + V2 + V3; V = 7 вольт. |
Изобразим это помощью векторов.
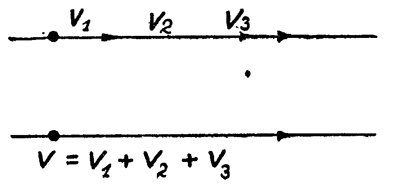
Единицу масштаба оставим ту же, 1 вольт соответствует 1 см. На рис. 5 ясно видно, что общее напряжение батареи
| V = V1 + V2 + V3. |
Эти две задачи мы решили двумя способами — алгебраическим и графическим.
Достоинство графического метода заключается в его наглядности. В самом деле, изобразив напряжение векторами, мы совершенно ясно видим взаимодействия напряжений между собой и их сумму.
Рассматривая этот пример, видим, что для того, чтобы найти сумму несколько одинаково направленных векторов, их величины нужно сложить.
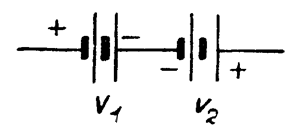
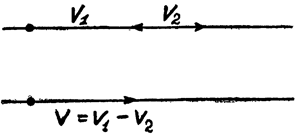
Теперь найдём сумму противоположно направленных векторов. Решим такую задачу. Имеются две батареи V1 = 5 в. и V2 = 2 в., включенные навстречу друг другу (рис. 6).
Нужно найти общее напряжение V.
| V = V1 — V2; V = 5 — 2; V = 3 в. |
Решим эту же задачу помощью векторов.
В данном случае оба вектора имеют противоположные направления, так как электродвижущие силы направлены навстречу друг другу. Из рис. 7 ясно видно, что электродвижущие силы батарей противоположны. Остается только найти результирующую эдс.

Совершенно очевидно, что
| V = V1 — V2. |
Сделаем вычитание отрезков графически. Для этого совместим отрезки так, как изображено на рис. 8. Кусочек, оставшийся от отрезка V1, есть общая электродвижущая сила V.
Теперь разберем случай, когда оба вектора равны по абсолютной величине, но обратны по направлению. К этому сводится задача для того случая, когда нужно найти общее напряжение V двух батарей, если электродвижущие силы их равны, но противоположны по знаку (см. рис. 9). На рис. 10 мы найдем графическое решение этого вопроса. Совместив векторы, мы получим в результате нуль.
| V = V1 — V2 = 0. |
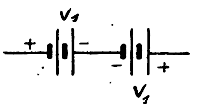
Из разобранных примеров видно, что в том случае, когда векторы имеют противоположное направление, результирующий вектор равен разности их абсолютных величин и имеет направление большего вектора, (большего по абсолютной величине).
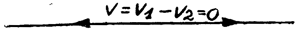
Теперь разберем способ нахождения суммы, или, как говорят, результирующей (или равнодействующей) двух векторов в том случае, когда они расположены под углом. С этим случаем мы довольно часто встречаемся в радиотехнике. Мы же разберем этот случай на взаимодействии двух сил. Если бросить камень в горизонтальном направлении, то камень вовсе не летит горизонтально, а летит по какой-то кривой и через некоторое время падает на землю. Это происходит от того, что на камень, кроме той силы, с которой мы его бросили, действует сила притяжения земли, действующая вниз. Чем камень будет тяжелее, тем эта сила будет больше, и камень упадет скорее на землю. Построим графически взаимодействие этих сил.
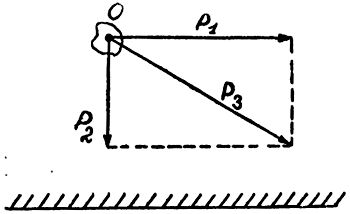
Сила P1 есть сила, с которой мы бросили камень. Сила Р2 — сила притяжения земли. Результирующая сила Р3 получается в результате так называемого геометрического сложения сил. Сложение это производится следующим образом. От конца силы Р2 проводят линию параллельно направлению силы Р1, а от конца силы Р1 проводят тоже линию, параллельную силе Р2. Точку приложения сил 0 соединяют с точкой пересечения этих линий, а линия ОА и даст нам по величине и направлению результирующую силу Р3. Величина равнодействующей Р3 может быть определена прямо по масштабу, в котором были построены силы Р1 и Р2. Под влиянием этой равнодействующей камень, пролетев некоторое время над землей, упадет на нее.
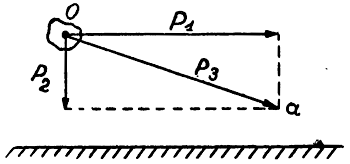
Чем с большей силой мы бросим камень, тем он дальше полетит, так как тогда равнодействующая будет направлена менее наклонно к земле (см. рис. 12).
Вообще, когда мы имеем два вектора разного направления, то их равнодействующая является диагональю четырехугольника (см. рис. 11 и 12), полученного от проведения параллельных линий от концов сил. Такой четырехугольник называется параллелограммом.
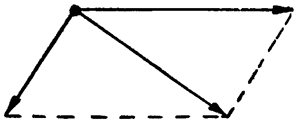
В том случае, когда векторы направлены не под прямым углом, равнодействующая может быть найдена до тому же самому правилу (см. рис. 13). Руководствуясь этим правилом, можно найти равнодействующую 3 векторов (рис. 14).
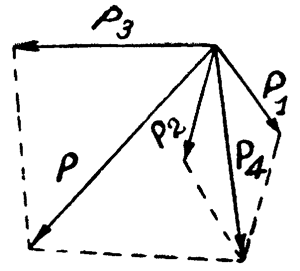
Для этого прежде всего складываются векторы P1 и Р2. Полученный равнодействующий вектор Р4 складывается с вектором Р3, и мы получаем результирующий вектор Р. Пользуясь этим способом, можно найти равнодействующую и большего числа векторов.
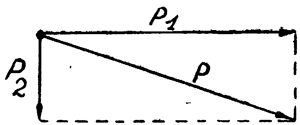
В том случае, когда, угол между векторами прямой (см. рис. 15), величина равнодействующей легко может быть найдена вычислением:
| P2= P21 + P22; Р = √ | P21 + P22 |