

Инж. А. Н. Попов.
Мы познакомились с двумя видами сопротивлений в цепи переменного тока: омическим и индуктивным. Есть еще одно сопротивление, именно емкостное. Это сопротивление, которое создаст в цепи конденсатор, в нее включенный. Прежде чем перейти к разбору общей цепи переменного тока (рис. 1). т. е. такой, где имеются все три вида сопротивлений, мы остановимся на том, что будет происходить в конденсаторе, если его приключить к зажимам источника переменного тока, как показано на рис. 2.
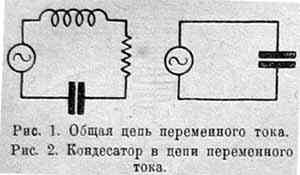
Ранее мы разбирали ("Р. В." №17) мгновенный ток смещения в конденсаторе. Для понимания того, что будет происходить при переменном напряжении, нужно только вспомнить, что оно все время меняется по величине. Количества электричества на обеих обкладках все время меняются, в диэлектрике все время будет ток смещения а в остальной цепи ток приводимости. Когда эдс (2) изменит направление, явление смещения и движения электронов от этого не нарушится.
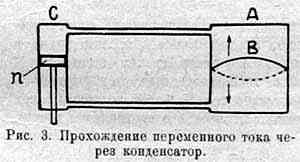
Таким образом переменный ток проходит через конденсатор. Обычно это поясняют, как показано на рис. 3. В цилиндре С ходит поршень П. Цилиндр соединен двумя трубами с баком А, в котором натянута перепонка В. Все заполнено водой. Если мы будем двигать поршень в одном направлении, скажем вниз, его действие на частицы воды будет примерно то же, что постоянный эдс на электроны. Вода двинется вверху — от А к С, внизу — наоборот. Перепонка (мы, конечно, предполагаем, что она воды не пропускает) выпучится кверху. Остановим поршень. Картина будет соответствовать накоплению электричества на конденсаторе от источника постоянного тока. Выпученная перепонка изобразит поляризованный диэлектрик. Если передвинуть поршень в крайнее верхнее положение, перепонка выпучится книзу: электричества на обкладках переменили знак; диэлектрик поляризовался в обратном направлении.
Теперь будем двигать поршень вверх и вниз. Вода в нашей системе будет колебаться (двигаться туда и сюда), причем перепонка это движение не остановит (движение в одном направлении она бы остановила). Это и изобразит переменный ток через конденсатор.
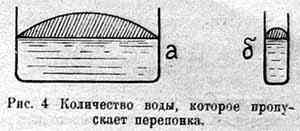
Возникает вопрос: как проявит себя конденсатор по отношению к источнику эдс? Очевидно, если бы мы поставили перепонку не в большом резервуаре А, а, скажем, в верхной трубке, то есть сделали бы ее очень маленькой, она бы сильно стесняла движение воды. Действительно, из рис. 4 видно, что в одном случае (а) в движении участвует вода, заключенная под "крышей" большой перепонки (заштрихована); в другом случае (б) движется некоторое количество воды. Итак, чем больше перепонка, тем больше ее пропускная способность. Далее, очевидно, играет роль упругость перепонки. Чем она больше может выпучиваться, тем, опять-таки, большее количество воды поместится под ней и будет двигаться взад и вперед. Размеры перепонки и ее упругость в применении к конденсатору будут означать его емкость; размеры перепонки — величину обкладок, ее упругость диэлектрическую постоянную.
Таким образом мы можем получить различную пропускную способность конденсатора. Уменьшение же этой способности означает увеличение сопротивления. Итак, конденсатор вносит «емкостное» сопротивление в цепь переменного тока, причем это сопротивление тем меньше, чем больше емкость конденсатора.
Вспомним, что силу тока мы определяем как количество электронов, прошедших в одну секунду через какое-нибудь место в цепи. В переменном токе мы не будем считаться с направлением, в котором движутся электроны, а будем их все «валить в одну кучу». Очевидно, тогда через наш конденсатор их пройдет тем больше, чем больше частота эдс. Поэтому емкостное сопротивление уменьшается с увеличением частоты. Один и тот же конденсатор будет обладать большим сопротивлением для токов низкой частоты (напр. 50 пер/сек) и небольшим для радиочастотных токов.
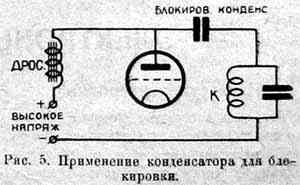
На том свойстве конденсатора, что он пропускает переменный ток и запирает постоянный, основаны его многочисленные применения для так называемой «блокировки». На рис. 5 показана схема с так наз. «параллельным питанием». Если бы не было блокировочного конденсатора, батарея высокого напряжения замкнулась бы через очень маленькое сопротивление катушек Др. и К, через нее пошел бы очень большой ток, который пережег бы катушки и испортил батарею. Для избежания этого ставят блокировочный конденсатор: он препятствует прохождению постоянного тока, а токи радиочастоты, которые получаются в контуре, пропускает свободно.
Наоборот, катушка с большой самоиндукцией (так называемый дроссель) Др. представляет большое сопротивление для токов высокой частоты и свободно пропускает ток постоянный.
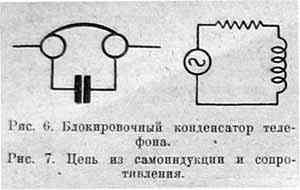
Блокировочный конденсатор, который приключают к телефону (рис. 6), служит для того, чтобы отвести от телефона высокую частоту и дать на него только звуковую.
Нужно заметить, что конденсатор никакой энергии от источника не забирает: его сопротивление также безуаттно, как и сопротивление индуктивное.
Вернемся к цепи рис. 1. Если мы захотим узнать силу тока в ней, то нам придется учесть все три вида сопротивлений: омическое, индуктивное и емкостное. Здесь выступает любопытное свойство наших двух безуаттных сопротивлений. Оказывается, что они действуют друг против друга: когда одно противодействует источнику тока, другое ему помогает, и наоборот. Входить в подробное объяснение этого явления мы здесь не можем, и ограничимся только упоминанием о самом факте. На основании только что сказанного будет понятно, почему одному сопротивлению (принято индуктивному) приписывают знак плюс, а другому — емкостному, знак минус. Таким образом, они всегда вычитаются одно из другого.
Если в цепи из сопротивления и самоиндукции (рис. 7) течет ток определенной силы, мы можем его увеличить, включивши последовательно конденсатор. Если мы его емкость сделаем слишком маленькой, то емкостное сопротивление перетянет индуктивное и сила тока опять уменьшится.
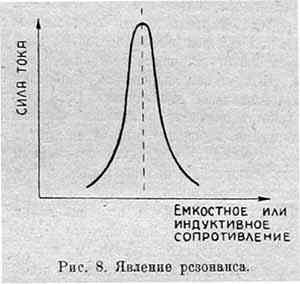
Спрашивается, что будет, если емкостное и индуктивное сопротивления как раз равны друг другу? В этом случае наступит то явление, которое называется резонансом: наши безуаттные сопротивления уравновесят друг друга и сила тока будет такова, как если бы было одно лишь омическое сопротивление. В этом случае она имеет наибольшее из всех возможных значений. Сила тока около резонанса нарастает и спадает (в зависимости от какого-либо безуаттного сопротивления) очень быстро. Это показано на рис. 8. По горизонтальной оси отложено какое-либо из безуаттных сопротивлений, по вертикальной — сила тока. Пунктир соответствует «резонансному» сопротивлению. Кривая вздымается тем круче и «пика» верщины ее тем выше (т. е. сила тока возрастает тем быстрее и достигает тем большей величины), чем меньше омическое оопротивление в цепи.

1) См. "Р. В" № 2.
2) Эдс — сокращенное обозначение электродвижущей силы.