

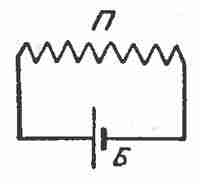
Закон Ома, с которым уже знакомы наши читатели, дает зависимость между напряжением на концах проводника (V), его сопротивлением (R) и силой тока, протекающего по проводнику (I). По этому закону V = IR, то-есть напряжение на концах проводника равно силе тока в проводнике, умноженной на его сопротивление. Например, если мы имеем проводник, П, имеющий сопротивление в 10 ом, включенный на батарею Б, дающую напряжение в 1 вольт (рис. 1), то сила тока в проводнике будет равна 1/10 ампера. Напряжение же на концах будет 1/10 ампера × 10 ом = 1 вольт, то-есть, как раз равно напряжению батареи Б. Но так оно и должно было бы быть, так как к концам проводника как раз приложено напряжение батареи, дающей один вольт.
Теперь рассмотрим цепь, состоящую из той же батареи и двух проводников П1 и П2, включенных последовательно (рис. 2). Если, например, проводник П1 имеет сопротивление в 10 ом, а проводник П2 — сопротивление в 30 ом, то общее сопротивление всей цепи составит 40 ом, и сила тока в ней будет равна 1/40 ампера. Напряжение же на концах проводника П1 по закону Ома будет составлять 1/40 ампера × 10 ом = 1/4 вольта, а напряжение на концах проводника П2 будет 1/40 ампера × 30 ом = 3/4 вольта. Вместе оба эти напряжения составят 1/4 вольта + 3/4 вольта = 1 вольт, то-есть, как раз то напряжение, которое дает батарея. Но напряжение, которое приходится на определенный участок цепи, например на участок П1 или П2, будет различно для различных участков цепи и будет зависеть от сопротивления этого участка. Чем больше сопротивление какого-либо участка цепи, тем больше напряжение, приходящееся на этот участок. Например, в нашем случае на участок П2, имеющий сопротивление в 30 ом, приходится напряжение в 3/4 вольта, а на участок П1, имеющий сопротивление в 10 ом приходится напряжение в 1/4 вольта.

То напряжение, которое приходится на какой-либо участок цепи, по которой течет ток, называется падением напряжения на этом участке цепи. Звачит в нашем случае мы имеем на участке П1 падение напряжения в 1/4 вольта, а на участке П2 — падение напряжения в 3/4 вольта. Конечно, падение напряжения во всей цепи, то-есть сумма падений напряжения на всех ее отдельных участках, как раз равно тому напряжению, которое дает источник электричества, включенный в цепь (в нашем случае батарея Б).
Тем обстоятельством, что напряжение, даваемое батареей распределяется на отдельные участки цепи, в которую эта батарея включена, можно воспользоваться для того, чтобы разделить напряжение батареи и получить только часть этого напряжения. Приборы, которые служат для этой цели называются делителями напряжений или потенциометрами.

Представим себе проводник, имеющий сопротивление R и включенный на батарею Б, дающую напряжение V (рисунок 3). На концах этого сопротивления мы будем иметь все напряжение V, даваемое батареей. Но вдоль проводника это напряжение распределится равномерно, и на участок его АБ, составляющий одну пятую часть всего проводника, придется всего одна пятая часть напряжения, даваемого батареей. Так что, если мы устроим ползунок П, двигающийся вдоль проводника, то падение напряжения между точками А и П будет зависеть от положения ползунка. Чем ближе ползунок к точке А, тем меньше участок цепи, лежащий между этими точками и тем меньше сопротивление этого участка цепи. А значит тем меньше и напряжение между этими точками. Наоборот, чем дальше мы отодвинем ползунок П от точки А, тем больше будет этот участок цепи, тем больше будет его сопротивление, а значит тем больше будет и падение напряжения на этом участке. Если мы передвинем ползунок до самого конца, к точке В, то между точками А и В будет включено все сопротивление R и, значит, напряжение между этими точками будет как раз равно всему напряжению, даваемому батареей. Таким образом передвигая ползунок П вдоль проводника R, мы можем между точками А и П получить любые напряжения, начиная от самых малых и кончая тем, которое дает батарея. (Но получить при помощи потенциометра напряжение большее, чем дает батарея, конечно, невозможно).

Вместо потенциометра с ползунком, который мы описали только что, можно в качестве делителя напряжения применить декадный магазин сопротивлений, который был описан в прошлом № журнала и постройка которого составляла практическую работу к прошлому занятию.
Если, например, одну группу этого магазина, состоящую из десяти сопротивлений, замкнуть на батарею, дающую 1 вольт, то на концах одного из этих сопротивлений (точки А и Б на рис. 4), можно получить 1/10 вольта, на концах двух из этих сопротивлении (А и В) 2/10 вольта и т. д. Включив две группы сопротивлений последовательно, например группы в 1 и 10 ом, так чтобы общее сопротивление всей цепи составляло 100 ом, т.-е. 10 сопротивлений 1-ой группы и 9 сопротивлений 2-ой группы (рис. 5), можно напряжение, даваемое батареей, разделить еще на более мелкие части. Например, между точками А и Б мы получим напряжение в 1/100 вольта, между точками А и В в 2/100 вольта и так далее. Если мы включим в цепь батареи все три группы сопротивлений магазина, так, чтобы общее его сопротивление составляло 1.000 ом, то на участке в 1 ом мы получим напряжение в 1/1000 вольта, на участке в 2 ома (между точками А и В) мы получим напряжение в 2/1000 вольта и т. д.

Таким образом, построенный нами магазин сопротивлений может служить не только в качестве реостата, но и в качестве потенциометра, позволяющего делить напряжения на десятые, сотые и тысячные доли. Дальнейшие указания о применении этого декадного магазина читатель найдет в практической работе к этому и следующим занятиям.
Мы уклонимся немного в сторону, чтобы рассмотреть один вопрос, который имеет очень большое значение. При рассмотрении цепи, которая состоит из батареи Б и проводника П (рис. 1), мы все время принимали во внимание только сопротивление проводника. Но фактически сопротивлением обладает не только проводник П, но и батарея Б. Это сопротивление батареи называется ее внутренним сопротивлением, причем величина внутреннего сопротивления батареи зависит от ее типа и размеров. Чем больше батарея, тем меньше ее внутреннее сопротивление. Но все же при рассмотрении электрических цепей, как бы ни было мало внутреннее сопротивление батареи, в некоторых случаях, чтобы не впасть в ошибку, необходимо это сопротивление учитывать.
Если в цепи, состоящей из батареи Б и провода П, принять во внимание не только сопротивление провода R, но и внутренее сопротивление батареи Rb, то полное сопротивление цепи будет (R + Rb) ом. По закону Ома сила тока в этой цепи будет
| I = | V |
| R + Rb |
т.-е. меньше, чем та сила тока, которая получилась бы, если бы мы принимали во внимание только сопротивление проводника.
Тоже самое можно сказать и про падение напряжения на отдельных участках цепи. Падение напряжения на концах проводника П равно IR, а падение напряжения внутри самой батареи IRb (так как батарея наша обладает сопротивлением, то в ней, как и во всяком проводнике, происходит падение напряжения). Но, как мы уже говорили, сумма падений напряжения на отдельных участках цепи равна напряжению, даваемому батареей. Это значит, что часть напряжения, даваемого батареей IRb, пропадает в самой батарее в виде внутреннего падения напряжения. Чем больше внутреннее сопротивление батареи, и чем больше сила тока в батарее, тем больше внутреннее падение напряжения у батареи.
Значит от батареи, имеющей данное сопротивление, нельзя брать какой угодно большой ток. Если ток, даваемый батареей очень велик, то и внутреннее падение напряжения будет так велико, что остаток напряжения, приходящийся на внешнюю цепь (так называемое рабочее напряжение батареи), будет очень мало. Только в том случае, если внешнее сопротивление в цепи (R) очень велико по сравнению с внутренним сопротивлением батареи (Rb), можно не принимать во внимание внутреннего сопротивления батареи.