

Мы имеем 3 последовательно включенных сопротивления (рис. 3) и нам нужно узнать общую величину сопротивления цепи. Для этого нам придется сложить величины всех сопротивлений, и полученная сумма даст нам результат
Это решение годится для данного частного случая. Если же мы хотим вывести общую формулу, то надо обозначить сопротивления буквами и уже с буквами оперировать (рис. 4).
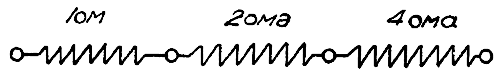
У нас имеется цепь, в которую включены последовательно 3 сопротивления: R1, R2, R3; требуется узнать общую величину сопротивления цепи. Обозначив искомую величину через R, мы имеем
Это уже не решение частного случая, а общая формула для любых численных значений включенных сопротивлений. Теперь попробуем воспользоваться нашей формулой. Предположим, что R1 = 3 омам, R2 = 5 омам, R3 = 6 омам, тогда R = 3 ома + 5 ом + 6 ом; R = 14 омам.
Если R1 = 12 омам, R2 = 3 омам, a R3 = 0,5 ома то R = 12 ома + 3 ома + 0,5 ома; R = 15,5 ома.
Полученная нами формула действительна для любых численных величин трех последовательно включенных сопротивлений.
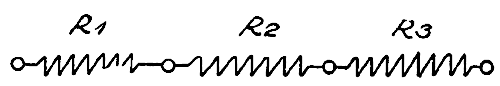
Из разобранного примера видно, что метод буквенных обозначений — алгебраический метод — имеет несомненное преимущество перед методом непосредственной работы с числовыми величинами, практикуемым в арифметике. Алгебраическое решение задачи дает нам формулу с буквенными выражениями, взамен которых затем подставляются числовые величины (так же, как в примере с сопротивлениями). Для того чтобы уметь читать формулы и вычислять по ним, надо научиться действиям с буквенными выражениями.
Алгебраическим выражением называется совокупность букв и чисел, соединенных между собой знаками действий.
Те алгебраические выражения, в которых конечными действиями не является сложение и вычитание, называются одночленами.
Например:
| N; | а × d; | с | ; — | b · k | ; |
| d | x |
Знак умножения обычно пишется в виде точки, а между буквами совсем не пишется.
Если рядом стоят несколько букв, например a, b, c, то это значит, что они перемножаются. Знак деления обычно. пишется в виде дробной черты,
| a | . |
| b |
Если перед одночленом не стоит никакого знака, то он считается положительным, если же стоит знак минус, то он считается отрицательным.
Многочленом называется совокупность одночленов, например:
| ab + c; | C | + ab; |
| d |
Коэффициентом называется числовой множитель, стоящий впереди буквенного выражения.
Например: 3а, 5ab и т. д. (3 и 5 — коэффициенты).
Коэффициент показывает, сколько раз слагаемым берется выражение, перед которым он стоит. Например: 3а представляет собой a + a + a, 5ab это ab + ab + ab + ab + ab, т. е. пять раз ab.
Подобными членами называются члены, отличающиеся только коэффициентами.
Например: 3ab; ab; 19ab будут подобными членами, так как отличаются только коэффициентами. Выражение
| 3cd и 3 | с |
| d |
подобными членами не будут, так как знак действия разный — в первом случае умножение, а во втором — деление.
Если в данном выражении имеется несколько подобных членов, то их объединяют, или, как говорят, делают приведение подобных членов. Для приведения подобных членов нужно взять алгебраическую сумму их коэффициентов и приписать к ней прежнее выражение.
Примеры:
В больших выражениях подобные члены нужно как-нибудь отличать (например подчеркиванием одной или двумя линиями) для того, чтобы при приведении не пропустить какое-либо выражение.
Б. Малиновский