Обращаем особое внимание радиолюбителей на описываемую ниже систему конденсатора с переменной емкостью и приглашаем их поработать над наиболее простой его конструкцией для любительского изготовления; особенно важно поработать над конструкцией такого конденсатора с воздушным диэлектриком. Необходимо обратить серьезное внимание на изоляцию: она должна быть хороша, чтобы конденсатор давал минимальные потери; это особенно важно при работе с короткими волнами. Ред.
В последнее время за границей все большее распространение приобретает переменный кондепсатор особой конструкции, называемой по английски "Squarelaw condenser", по французски "condensateur suivant la loi du carré". Наиболее подходящим для этой конструкции русским названием будет "квадратичный конденсатор".

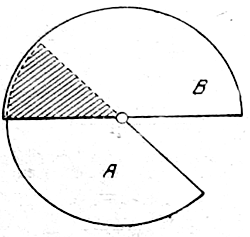
Для того, чтобы яснее представить себе принцип действия и особенности этого конденсатора, остановимся несколько для сравнения на работе обычного переменного конденсатора с полукруглыми пластинками. Допустим, что этот конденсатор имеет только две пластины — одну подвижную А, другую неподвижную В (рис. 1). Как известно, емкость конденсатора определяется формулой
| С = | KS | , |
| 4π d |
где буквой F 1) обозначена площадь работающей части пластин, заштрихованная на нашем рисунке. Из рисунка мы видим, что если подвижную пластинку повернуть на угол вдвое больший (положим с двадцати делений на сорок), то и работающая поверхность пластин увеличится вдвое; при увеличении угла вращения втрое, площадь конденсатора увеличится также в три раза и т. д. Из формулы же, которая написана выше, мы видим, что во сколько раз увеличится площадь конденсатора (S), во столько же раз увеличится и емкость его. Сопоставляя оба эти обстоятельства, мы можем сказать, что емкость конденсатора с полукруглыми пластинами изменяется в столько же раз, во сколько изменяется угол поворота, т.-е. емкость такого конденсатора пропорциональна углу поворота его пластин. Но при работе с настраивающимися приемными или передаточными контурами нам удобнее и проще оперировать с длиной волны, чем с емкостью.
Как же изменяется длина волны контура при вращении ручки переменного конденсатора? Для ответа на этот вопрос обратимся к основной формуле для длины волн:
| λ = 2π √L · C. |
Мы видим, что при постоянной самоиндукции L и переменной емкости С длина волны не изменяется пропорционально изменению емкости — длина волны пропорциональна квадратному корню из величины емкости: так, если емкость данного контура увеличится в 2 раза, то длина волны его увеличится лишь в √2 раза, т.-е. в 1,4 раза; при изменении емкости в 4 раза, длина волны изменяется в √4, т.-е. в 2 раза и т. д. Следовательно, изменяя положение пластин в переменном конденсаторе обычного типа, мы при равномерном вращении ручки конденсатора, получим равномерное изменение емкости, но не получим равномерного изменения длины волны контура.
Как же достичь равномерного изменения длины волны по всей шкале конденсатора? Для этого нужно, чтобы емкость изменялась не пропорционально углу поворота пластин, как это было до сих пор, но пропорционально квадрату этого угла, т.-е., при изменении, напр., угла поворота вдвое, емкость должна измениться в 22, т.-е. в 4 раза, при изменении угла в 3 раза, емкость должна измениться в 32, т.-е. в 9 раз и т. д. Соответственно длина волны будет изменяться в √4 = 2, √9 = 3 раза и т. д. т.-е. получается изменение длины волны равномерное по всей шкале конденсатора.
Для того, чтобы осуществить такое изменение емкости, какое там необходимо, нужно дать пластинам переменного конденсатора такую форму, чтобы при вращении их площадь изменялась пропорционально квадрату угла поворота. Таким свойством обладает пластина, изображенная на рис. 2. Ее очертание можно получить следующим образом:
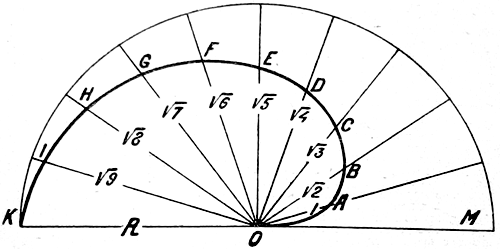
Задаемся прежде всего основным размером R, т.-е. величиной отрезка OK; примем его равным, напр., 60 мм. На листе бумаги произвольным радиусом очерчиваем половину окружности и делим ее на несколько равных частей. В нашем примере дуга разделена на 10 частей. Соединяем центр О радиусами со всеми этими точками. Вся кривая построена таким образом, что расстояние r любой точки ее от точки О равно
| r = R | √ | θ | , |
| π |
где R есть величина выбранного нами наибольшего отрезка ОК, а θ — угол, составленный отрезком ОМ и радиусом r, причем угол этот выражен в долях π.
Так как в нашем примере полуокружность разделена на 10 частей, то угол, составленный первым радиусом ОА с прямой ОМ, равен π / 10; следовательно, для этого случая θ = 0,1 π; так как ОК или R мы приняли равным 60 мм., то имеем, что
| OA = 60 | √ | 0,1 π | = 19 мм. |
| π |
Остальные точки отыскиваются следующим образом: отрезок ОВ равен первому отрезу ОА, увеличенному в √2 раз. Так как ОА равен 19 мм., a √2 равен 1,414, то
| ОВ = ОA √2 = 19 · 1,414 = 26,9 мм. |
Точно так же определяется следующий отрезок ОС, ранный ОА √3, то-есть 19 · 1,732 = 32,9 мм. Остальные радиусы ОD, ОЕ, OF и т. д. равны тому же начальному отрезку ОА, увеличенному соответственно в √4, √5, √6 и т.д. раз, т.-е. OD = ОА√4, ОЕ = ОА√5 и т. д.
Для облегчения расчетов привожу таблицы величин квадратных корней для первых 20 чисел (см. ниже).
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Квадр. корень. | 1 | 1,414 | 1,732 | 2 | 2,236 | 2,449 | 2,645 | 2,828 | 3 | 3,162 |
| Число | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Квадр. корень. | 3,316 | 3,464 | 3,605 | 3,741 | 3,872 | 4 | 4,123 | 4,292 | 4,358 | 4,472 |
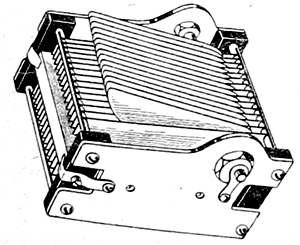
Когда таким образом найдены все точки А, В, С, D, Е, F, G, H, I, К, то остается только соединить их плавной кривой, по ней вырезать лист, и форма подвижной пластины квадратичного конденсатора определена. В собранном виде конденсатор представлен на рис. 3. Число пластин берется в зависимости от желаемой величины емкости конденсатора и промежутка между пластинами.
Площадь той части пластины, которая вошла в промежуток между неподвижными пластинами при повороте ручки конденсатора на некоторый угол θ, можно найти из формулы:
| F = | R2 θ2 | , |
| 4π |
где R есть величина максимального радиуса, а θ угол поворота, выраженный в долях π. Для того случая, когда пластина вошла полностью, т.-е. когда θ = π, площадь
| F = | π R2 | ≈ 0,785 · R2. |
| 4 |
Рассматривая формулу
| F = | R2 θ2 | , |
| 4π |
мы видим, что площадь работающей части пластин пропорциональна квадрату угла поворота, т.-е. при увеличении этого угла в 2 раза площадь увеличится в 22 = 4 раза, при увеличении угла втрое площадь увеличится в 32, т.-е. в 9 раз, и т. д. Емкость конденсатора будет изменяться в такой же пропорции, а, следовательно, длина волны, пропорциональная квадратному корню из емкости будет изменяться в √4 = 2, √9 = 3 и т. д. раза, т.-е. так же, как изменялся угол поворота пластин.
Допустим, что, имея определенную катушку самоиндукции, мы настроились на волну Сокольников (1010 мт.) при повороте шкалы квадратичного конденсатора на 30°. Длина волны ст. им. Коминтерна 1450 мт. в 1,43 раза больше волны Сокольнической станции; следовательно, мы можем заранее сказать, что при этой же самоиндукции настроимся на станцию им. Коминтерна, увеличив угол в 1,43 раза, т.-е. повернув ручку конденсатора приблизительно на 43°.
К числу достоинств квадратичного конденсатора нужно отнести также чрезвычайно небольшую величину его начальной емкости.
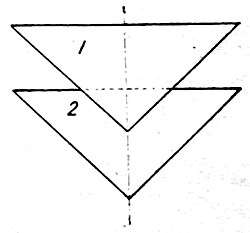
В заключение заметим, что тот же квадратичный закон изменения емкости может быть получен при пластинах и другой формы. На рис. 4 изображены, напр., пластины трехугольной формы. При передвигании подвижной пластины (1) относительно неподвижной (2) емкость будет увеличиваться пропорционально квадрату расстояния, на которое пластина передвинулась. Механизм передвигания можно, конечно, привести к вращению ручки на 180°. Применяются также пластины, имеющие форму ромба.
1) В разных местах заметки площадь работающей части пластин конденсатора обозначается как буквой F, так и буквой S. В статье буквенные обозначения оставлены так, как они напечатаны в журнале. (прим. составителя). (стр. 310.)