

Закон больших чисел дает новое и в высшей степени важное освещение математической вероятности. Что следует из того, что вероятность выиграть у одного игрока равна ⅔, а у другого ⅓? Здравый смысл подсказывает такой ответ: из этого следует, что выиграет скорее первый, чем второй. Ничего более определенного об исходе одной-двух партий сказать невозможно. Но если игроки сыграют очень большое число партий (например, 10000), то, по закону больших чисел, первый почти наверное выиграет около ⅔ всех партий, а второй около ⅓. Поэтому, если ставки игроков равны, первый почти наверное обыграет второго. Такая игра не безобидна: из двух игроков, которые согласились играть на таких условиях, один вовлек другого в невыгодную сделку.
Игра в орлянку — при равных ставках — безобидная игра. В ней совершенно невозможно предвидеть, кто кого обыграет. Вообще безобидной принято называть такую игру, исход которой, даже при очень большом числе партий, невозможно предвидеть.

Для этого вовсе не обязательно, чтобы шансы игроков были равны. Неравенство шансов можно компенсировать разными размерами ставок. Если, например, у одного игрока вероятность выиграть равна ⅔, а ставка его 6 рублей, а у другого вероятность выиграть ⅓ и ставка 3 рубля, то при очень большом числе партий (скажем, 10000) можно ожидать, что первый выиграет около ⅔ × 10000 партий (это даст ему выигрыш около ⅔ × 10000 × 3 = 20000 рублей), а второй выиграет около ⅓ × 10000 партий, и выигрыш его будет равен около ⅓ × 10000 × 6 = 20000 руб. Вероятные выигрыши обоих приблизительно равны; невозможно предвидеть, кто кого обыграет. Значит, игра безобидна. Вообще, для безобидности игры необходимо, чтобы произведение из ставки каждого игрока на вероятность его выигрыша было равно произведению из ставки его партнера на вероятность его выигрыша. Это произведение называют математическим ожиданием игрока. Рулетка и ей подобные клубные азартные игры не безобидны: содержатели клубов и казино озаботились тем, чтобы иметь немного больше шансов на выигрыш, чем предоставлено игрокам. Поэтому, например, рулетка в Монте-Карло, где математическое ожидение рулетки на ¹/₃₇ больше, чем следовало бы для безобидности, процветает и приносит огромные доходы акционерному обществу, которое ее содержит, и княжеству Монакскому, приютившему ее, а азартные игроки кончают полным раззорением во славу закона больших чисел. Благополучие рулетки всецело зиждется на этой ¹/₃₇; не нужно,
Даже безобидные игры большей частью доводят азартных игроков до разорения. В самом деле, допустим, что игрок обладает капиталом в 1000 рублей. Если он часто играет в безобидные игры, то одинаково вероятно, что он либо выиграет, либо проиграет 1.000 рублей. В первом случае — капитал его удвоился, во втором — он разорен и вынужден прекратить игру. Вероятность каждого из этих событий ½. Если это азартный игрок, то в первом случае он продолжает игру и может либо выиграть 2.000 руб. либо проиграть 2.000 рублей. Вероятность каждого из этих событий ½. Значит, вероятность, что игрок разорится либо при первой игре, либо при второй, равна ½ + ½ × ½ = ¾; а вероятность, что он, выиграв в первый раз, выиграет и во второй, равна ½ × ½ = ¼. Если игрок не разорен, он опять играет и либо снова удваивает свой капитал, либо теряет все. Как видите, разорение — более вероятная судьба игрока, чем обогащение. Профессиональный игрок имеет гораздо больше шансов стать нищим, чем богачом, потому что он подобен человеку, упорно добивающемуся разорения.
Широкая публика, обычно, хочет получить от теории вероятностей рецепт беспроигрышной игры в рулетку. Однако, никакая "система" не может увеличить шансы на выигрыш. Теория вероятностей может дать только один совет: бросить всякие надежды на "систему", а еще лучше бросить и самоё игру.
Рулетка в Монте-Карло, организованная при содействии многих выдающихся математиков, — одно из самых эффектных созданий теории вероятностей. Менее красочные на первый взгляд разнообразные страховые общества также всецело опираются в своих расчетах на эту теорию. Возьмем для примера страхование на случай инвалидности. Застрахованный уплачивает страховому обществу ежемесячно определенный небольшой взнос; за это общество обязуется обеспечить его в случае потери им трудоспособности определенной ежемесячной пенсией, которую он будет получать до самой смерти. В сущности, — это своего рода азартная игра, только более сложная, чем рулетка. Страховые взносы застрахованного — его ставки, страховая сумма — его выигрыш. Пока застрахованный здоров — он проигрывает ежемесячно свою ставку; если ему "посчастливилось" стать инвалидом — начинает выигрывать, и теперь проигрывает страховое общество; проигрыш его прекращается лишь со смертью клиента. Подобно рулетке, это игра не безобидная: математическое ожидание страхового общества всегда несколько больше математического ожидания клиентов, — в противном случае положение общества было бы весьма ненадежным, и оно не имело бы средств на содержание своего аппарата.
Размеры страховых взносов для каждой группы клиентов, в зависимости от их возраста и величины пенсии, на которую они претендуют, определяются, конечно, по методам теории вероятностей. Для этих расчетов необходимо знать вероятности того, что клиент потеряет трудоспособность в течение ближайшего года, двух лет, трех лет и т. д., а также вероятность того, что, потеряв трудоспособность, он проживет инвалидом на иждивении общества год, два, три и т. д. Эти вероятности нельзя определить наперед, теоретически, как при обычной игре. Но их можно установить, пользуясь статистикой смертности и инвалидности.
Если бы существовала определенная неизвестная нам вероятность человеку 20 лет стать инвалидом в ближайшем году, то, по закону больших чисел, из очень большого числа молодых людей 20 лет некоторая часть, равная приблизительно этой неизвестной вероятности, почти наверное должна была бы терять трудоспособность на 21-ом году жизни. Статистика показывает, что это действительно так и есть: из 100000 здоровых молодых людей указанного возраста становятся инвалидами на 21-ом году жизни около 20 человек: в одной группе из 100000 человек — 19, в другой — 22, в третьей — 17, в четвертой — 21 и т. д. Все это — числа, близкие к 20. Поэтому можно принять, что вероятность 20-летнему здоровому человеку потерять трудоспособность в ближайшем году равна приблизительно ²⁰/₁₀₀₀₀₀ = ¹/₅₀₀₀. Точно так же установлено статистикой, что из каждых 100000 здоровых молодых людей 20-ти лет умирают, не дожив до 21 года, приблизительно человек 900. Значит, вероятность для здорового 20-летнего человека умереть в ближайшем году равна приблизительно ⁹/₁₀₀₀. Далее статистика показывает, что вероятность инвалиду 20 лет умереть в ближайшем году равна приблизительно 0,1. Имея такие данные для всех возрастов, можно определить "ставки" страхуемого и общества. То обстоятельство, что страховые общества процветают, указывает на практическую надежность расчетов, на которых они строятся.
Любопытно, что в этом случае теория вероятностей отнюдь не предостерегает от участия в этой небезобидной игре. Конечно, если бы клиент страховался большое число раз, он почти наверное оказался бы в проигрыше. Но каждому суждено "сыграть в инвалидность и смерть" только однажды; поэтому теория вероятностей ничего не может сказать о выгодности или невыгодности этой игры. Здравый смысл подсказывает, что купить спокойную старость ценою незначительных взносов в молодости благоразумно и выгодно; теория вероятности не возражает.
Азартные игры были тем оселком, на котором, главным образом, заострялись методы теории вероятностей в течение 17-го и 18-го столетий. Во второй половине прошлого века эта теория нашла себе широкое применение в статистике, биологии и физике.
Изучая таблицы роста и объем грудной клетки новобранцев, антрополог Кетлэ обратил внимание на то, что уклонения от среднего роста и среднего объема грудной клетки встречались тем реже, чем они значительней, при чем замечалось удивительное постоянство в распределении людей по росту или по объему грудной клетки. Здесь наблюдается нечто подобное тому, что происходит при многократном бросании нескольких монет; если, например, бросают 4 монеты зараз, то чаще всего выпадают 2 орла (и 2 решетки), реже 1 или 3 орла и еще реже 0 или 4 орла, т. е. чаще всего, в согласии с законом больших чисел, вскрывается среднее число орлов, а уклонения от этого числа тем реже, чем они больше. Для уяснения этой аналогии воспользуемся примером, предложенным известным биологом Гальтоном. Гальтон построил прибор, изображенный на рис. 2. В верхнюю часть насыпают горох, затем открывают отверстие, и горошины скатываются вниз по наклонной доске; ударяясь о вбитые в нее гвозди. они уклоняются то вправо, то влево и, наконец, попадают в отделения нижнего ящика.
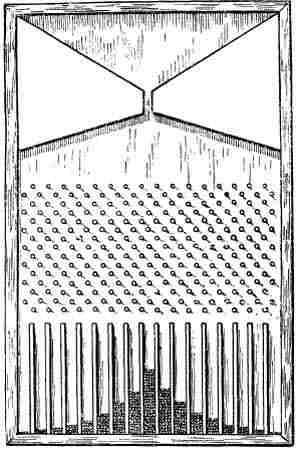
Вероятность того, что горошина будет все время уклоняться вправо (или влево) очень мала. Поэтому следует ожидать, что в крайние отделения ящика попадут только немногие горошины. Наиболее вероятно, что уклонения горошины вправо будут восполнены или почти восполнены уклонениями влево, так что чаще всего горошины будут попадать в средние отделения. Можно даже вычислить вероятности разных уклонений горошины вправо и влево и предвидеть вероятное распределение их в отделениях нижнего ящика.
Распределение людей по росту совершенно подобно распределению горошин в нижнем ящике прибора Гальтона. Сходство здесь не только качественное, но и количественное. Аналогичный закон распределения ("закон нормального распределения", как его называют) имеет место и во многих других случаях, с которыми приходится встречаться в биологии при изучении изменчивости растений и животных. Подобным же образом распределяются ошибки при измерениях: самые большие погрешности — результат случайного стечения многих обстоятельств, порождающих ошибки — встречаются всего реже. Таким образом, теория вероятностей находит себе применение в статистике, в биологии и при обработке результатов всевозможных измерений.
Мы видели, как широка область применения вероятности. Приятно, однако, сознавать, что наряду с областями, где господствуют нерешительные законы случая, имеются владения непреложных и точных закономерностей.

Если смешать вино с водой, получится разбавленное вино — более светлое, менее крепкое, чем чистое. Это случится не почти наверное, а наверное, крепость вина мы можем предвидеть не приблизительно, а точно. Однако, что происходит при смешении вина с водой? Физика учит нас, что вино подобно воде состоит из мельчайших подвижных частиц. Эти частицы движутся во все стороны среди частиц воды. Почему же не может случиться, что в какой-нибудь момент в одном месте сосуда соберется больше частиц вина, чем в другом? Почему в одно прекрасное мгновение частицы воды и вина не могут разделиться так, что справа, например, соберется вино, а слева чистая вода? На эти вопросы приходится ответить так: это не невозможно, но крайне невероятно. Количество частиц вина в 1 куб. мм вовсе не является постоянным: в одних местах оно больше, в других меньше, одни частицы улетают, другие прилетают на их место. Распределение в каждый момент подчинено тому же закону, который имеет силу для всех случайных явлений.
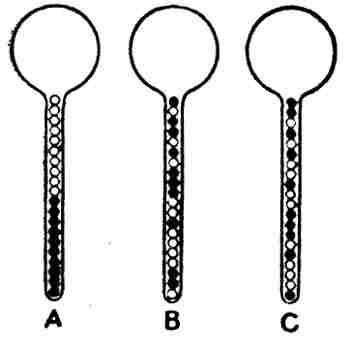
На рис. 4 изображена колба с узким горлышком, в котором лежит 10 черных и 10 белых шариков. Если перевернуть колбу, встряхнуть ее и снова опрокинуть горлышком вниз, шарики займут в ней места в каком-то новом, случайном порядке — черные и белые вперемешку. Если бы шарики были очень малы и число их очень велико, горлышко казалось бы нам заполненным чем-то серым. Сколько бы раз мы ни переворачивали нашу колбу, едва ли бы нам удалось добиться такого расположения шариков, чтобы все белые собрались внизу, а все черные наверху. Однако, такое разделение не невозможно, а только очень мало вероятно: вероятность его менее ¹/₂₀₀₀₀₀. В бутылке с вином частиц воды и вина не десятки, и даже не миллионы, а столь огромное число, что о нем трудно составить себе представление. Поэтому вероятность случайного разделения воды и вина так же, примерно мала, как вероятность того, что обезьяна, стуча без толку по клавишам пишущей машинки, отпечатает какой-нибудь роман.
Так называемая кинетическая теория материи показала, что многие, повидимому, непреложные явления на самом деле только очень вероятные исходы столкновения множества случайностей. Например, согласно этой теории нагретый воздух отличается от холодного только тем, что частицы его в среднем обладают большей скоростью. Но при всякой температуре одни частицы в данный момент движутся быстрее, другие медленнее. Количество тех и других подчинено "закону нормального распределения". Если бы случайно более быстрые частицы стали собираться, например, в одном углу комнаты, а медленные в другом, мы наблюдали бы, что одна часть комнаты сама собой нагревается, а другая остывает. Теоретически такое случайное скопление быстрых частиц в одном месте не невозможно, но очень мало вероятно, — настолько мало вероятно, что практически невозможно.
Чем шире охватывает научное исследование явления природы и жизни, тем больше закономерностей оно открывает. Но проникая глубже в эти явления, оно нередко обнаруживает в них хаос, сплетение миллиардов случайностей; порядок и строгая закономерность оказываются во многих случаях (а может быть и во всех?) только проявлениями закона больших чисел.
В заключение предложим нашим читателям произвести опытную проверку основного закона теории вероятностей — закона больших чисел. Для этого мы воспользуемся чрезвычайно интересной задачей известного французского натуралиста Бюффона. Задача заключается в следующем.
Лист бумаги разлинован рядом параллельных прямых на полосы одинаковой ширины. На него бросают иголку, длина которой равна ширине полосы. Какова вероятность, что иголка пересечет одну из линий, т. е. ляжет не целиком внутри одной полосы?
Чтобы решить задачу, установим прежде всего, что вероятнейшее число пересечений пропорционально длине иголки. Пусть при n бросаниях вероятнейшее число пересечений равно x. Разделим мысленно иголку на несколько, например, на 5, равных частей. При каждом пересечении иголки с одной из линеек точка пересечения лежит в одной из этих частей, при чем одинаково вероятно ее нахождение в любой из них. Поэтому вероятнейшее число пересечений ⅕ нашей иголки с одной из линий при n бросаниях равно ⅕ x. Для иголки, составляющей ⅗ данной, оно равно ⅗ x. И вообще, вероятнейшее число пересечений пропорционально длине иголки.
Теперь согнем иголку углом ABC (рис. 5). Пусть часть AB равна ⅗ иголки, а BC — ⅖. Бросим согнутую иголку n раз. Чему равно вероятнейшее число пересечений частью AB? Очевидно, ⅗ x. А частью BC — ⅖ x. Поэтому вероятнейшее число пересечений либо частью AB, либо частью BC попрежнему равно x (⅖ x + ⅗ x = x). В это число включены и такие случаи, когда иголка одновременно пересекает линию и частью AB, и частью BC, при чем каждый такой случай засчитан дважды: один раз он вошел в число ⅗ x случаев пересечения AB, а другой раз в число ⅖ x случаев пересечения BC. Таким образом, считая каждое двойное пересечение за два ординарных, мы получим для иголки, согнутой углом, такое же вероятнейшее число пересечений при n бросаниях, как и для прямой иголки. Подобным же рассуждением легко убедиться в том, что как бы мы ни сгибали иголку, вероятнейшее число пересечений при n бросаниях для нее не изменится, если только каждое двойное, тройное и т. д. пересечения считать за два, три и т. д. ординарных. Значит, вероятнейшее число пересечений пропорционально длине иголки и не зависит от ее формы.
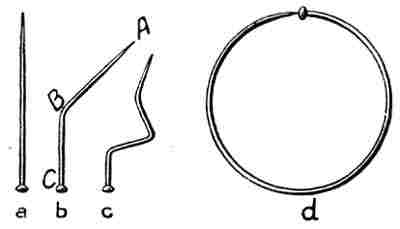
Представим себе теперь другую иголку, согнутую кольцом, как на рис. 6d. Пусть диаметр этого кольца равен как раз ширине полосы нашего листа. Тогда при каждом бросании кольцо пересечет одну из линеек 2 раза, а при n бросаниях — 2n раз. Кольцо ровно в π раз длиннее нашей иголки. Значит, вероятнейшее число пересечений для нашей иголки при n бросаниях в π раз меньше, чем для кольца, т. е. равно 2n/π. Стало быть, вероятность пересечения для нее равна 2n/π : n = 2/π.
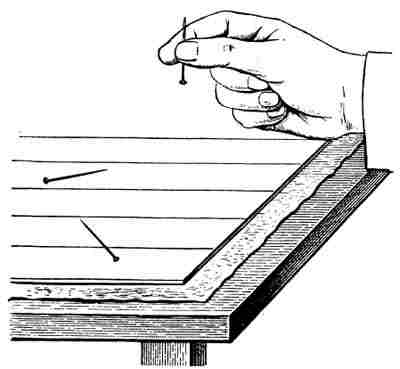
Этот неожиданный результат открывает возможность очень оригинального способа опытного определения числа π — путем бросаний иголки на линованный лист бумаги. По закону больших чисел при очень большом числе бросаний частота пересечений почти наверное будет мало отличаться от числа 2/π. Вот это-то я и предлагаю подвергнуть коллективной проверке. Вы должны взять лист бумаги, размером, приблизительно, 30 × 40 см и иголку длиной см 3—4, разлиновать бумагу так, чтобы промежуток между линейками был в точности равен длине иголки. Затем, положив лист бумаги на стол, убедитесь в том, что он лежит горизонтально и иголка не скатывается к какому-либо краю. Приготовьте карандаш и клочек бумаги, чтобы записывать результаты; каждое пересечение вы будете отмечать крестиком, отсутствие его — черточкой. Иголку перед бросанием держите вертикально, как показано на нашем рисунке. Чтобы гарантировать полную случайность бросаний, хорошо было бы производить их с завязанными глазами; в этом случае записывать результаты должен другой участник опыта, а бросающий до конца испытания не должен знать результатов.
Вы должны произвести всего 100 бросаний. Разультаты пришлите в редакцию нашего журнала, каковы бы они ни были. Имейте в виду, что 100 бросаний — не большое число, так что вероятность значительного уклонения числа пересечений от ожидаемого числа 200/π не очень мала; поэтому из одного вашего опыта нельзя делать никаких сколько-нибудь надежных выводов. Кроме того, очень значительное уклонение числа пересечений от ожидаемого мало вероятно, но не невозможно; поэтому среди многих сотен опытов, которые, — мы надеемся, — произведут наши читатели, найдется, вероятно, несколько таких, в которых уклонение будет весьма велико. Чрезвычайно интересно знать сколько окажется случаев разных уклонений — совпадет ли число их приблизительно с тем, которое следует ожидать по закону больших чисел.
Имейте в виду, что нет плохих результатов, бывает только плохая постановка опыта. Опыт поставлен хорошо, если лист бумаги лежит горизонтально и ровно (без бугров и впадин, куда иголка могла бы скатываться) если каждое бросание совершенно случайно, если всех бросаний ровно 100 и если результаты записаны и сообщены нам точно. Кто хочет, может произвести больше бросаний, но результаты должны быть подсчитаны и сообщены нам по каждой сотне отдельно. При обработке результатов мы будем принимать во внимание только опыты, содержащие полные сотни бросаний.

1) См. начало этой статьи в №2 нашего журнала. (назад)