"Природа", №04-06, 1919 год, стр. 243-252
Хотя в предлежащей маленькой статье автор по существу дела знакомит читателя с простым разрешением одного вопроса минералогии, до последнего времени представлявшегося ученым в высшей степени запутанным и почти неразрешимым, но, помещая ее в "Природе", автор льстит себя надеждой, что прочтение ее даст нечто гораздо большее.
Автор рассчитывает, что ознакомление с нею раскроет читателю во всем необъятном значении роль, которую играет в науке приведение сырого научного материала в строгий математический порядок. Она должна ярко представить читателю, как ничтожно значение самого обширного научного материала, даже когда на получение его затрачено непомерное количество труда при самом напряженном внимании к устранению всякого рода погрешностей, неточностей и ошибок, если только к этому материалу не прикоснулся хотя бы самый легкий труд особого рода, труд по приведению этого материала в особый порядок, вытекающий из глубины строгой, смело могу сказать, математической мысли.
В данном случае этот труд столь ничтожен в своем объеме сравнительно с трудом, затраченным на подготовительную, черновую работу сбора материала, произведенную не одним десятком именитых, отчасти даже знаменитых специалистов, каждый из которых положил на нее много недель своего драгоценного времени, что в смысле количества приложенных усилий, можно сказать, не прибавил ничего; но в смысле получения окончательного результата, в смысле извлечения из этого материала того закона природы, которому материал подчинен по существу дела, этот ничтожный прибавочный труд дал почти все; до его приложения материал находился подобно безформенной груде без всякого указания на ту жемчужину истины, которая в нем заключалась.
Мало того, из хода изложения, надеюсь, будет видно, что сравнительно с значением этого ничтожного добавочного труда, второстепенную или скорее не столь первостепенную роль играет точность обработки материала, как ни очевидно само по себе преобладающее значение именно точности обработки материала; ведь не может же подлежать сомнению, что для извлечения научной истины гораздо важнее иметь вдвое более точный материал (иначе сказать, материал, неизбежные неточности которого уменьшены вдвое), чем иметь вдвое больше материала. И тем не менее, тот особый, специализированный добавочный труд, о котором здесь упоминается, может сам по себе в значительной степени заместить с необычайной простотой тот окончательный, иногда каторжный по своему напряжению, труд, с которым бывает связано достижение наибольшей точности. Читателю, надеюсь, будет видно из изложения, что совершенно тот же точный научный результат получился бы от приложения добавочного труда даже при меньшей степени точности обработки сырого материала, при чем слишком уклонившийся от точности материал все равно выбрасывается, как совершенно негодный.
Научная минералогия появилась одновременно с кристаллографией и неорганической химией; счастливым образом эти две столь различные области точного знания появились одновременно (во второй половине XVIII века). И действительно, легко понять, как мало научности пришлось бы придать описанию минерала, если бы при этом в состав описания не вошли ни характеристика его кристаллографических особенностей, ни точное знание его химического состава.
В громадном большинстве случаев вопрос об его химическом составе разрешался весьма просто. Химия давала в руки технические средства производить разделение составных частей, которые можно было отдельно взвешивать, а введение понятия о наименьшей единице веса каждого отдельного простого химически отделенного вещества (его атомного веса) привело к отсчитыванию составных веществ в особых единицах, при чем оказалось, что пропорции веществ в таких единицах выражаются в целых числах, напр. поваренная соль выражается символом ClNa, то есть на единицу веса хлора приходится единица веса натрия, железная руда гаматит есть Fe2O3, то есть на две единицы железа приходится три единицы кислорода, минерал пирит (он же серный колчедан), из которого добывается серная кислота FeS2, то есть на единицу веса железа приходится две единицы серы и т. д.
Но рядом с преобладающим числом таких простых выражений для состава минералов получались и такие, которые находились между собой в непримиримом противоречии; что ни экземпляр — то особый состав, и вывести какой-нибудь простой закон, объединяющий состав минерала во всех его индивидах, казалось совершенно невозможным и нельзя было даже догадаться о причине того, отчего это происходит. Словом, для некоторых минералов не могло быть получено настоящего научного описания, так как, несмотря на обилие сырого материала, нельзя было никаким способом сколько нибудь удовлетворительно выразить их химический состав. К числу таких минералов относятся и хорошо известные в обыденной жизни слюды.
Сначала стали смотреть на них, как на совокупность различных минералов, которые, благодаря какой то случайности, имеют многие выдающиеся общие свойства. Но это представление скоро разбивалось не только о чувствительные уклонения в составе каждого такого минерала, взятого в отдельности, но и о присутствие столь разнообразных составов, что даже с самым грубым приближением нельзя было их подвести под определенные формулы химических составов.
Единственное, что удалось более или менее установить с научною точностью, это то, что они удовлетворяют выработанному химиками понятию об ортосиликатах (или, как выражались раньше, моносиликатах). Дело в том, что вообще весь состав слюд (как и силикатов вообще) можно представить себе разделенным на отдельные окислы (соединение металла с кислородом), а из составных окислов можно выделить четыре группы так называемых одноатомных, двухатомных, трехатомных окислов и четырехатомного окисла кремния или так называемого кремнезема, состав которого выражается формулою SiО2, или Si2O4. Этот окисел называется четырехатомным, потому что в нем один атом (единица веса) кремния Si насыщается двумя атомами кислорода О, а один атом кислорода, в свою очередь, насыщается двумя атомами водорода Н, почему кислород и относится к двухатомным химическим элементам, а кремний есть поэтому четырехатомный элемент, а его окисел Si2O4 есть четырехатомный окисел. Из трехатомных окислов в состав слюд входят глинозем А12O3 и окись железа Fe2O3; из двухатомных входят окись магния Mg2O2, отчасти закись железа Fe2O2 и в небольшом количестве другие, и, наконец, из одноатомных входят окиси калия К2О, водорода H2О (отчасти натрия Na2O и даже лития Li2О). И вот, ортосиликатами называются всякие такие группировки этих четырех групп окислов, при которых сумма единиц (или атомов) кислорода одна и та же, с одной стороны при кремнеземе, а с другой при всех остальных окислах; таковы например, сочетания Si2O4 + (K, Н)8O4 или проще Si(К, Н)4O4, где в скобках отмечается, что металл может быть безразлично представлен отчасти калием, отчасти водородом или же может быть сочетанием SiMg2O4 или напр. сочетанием Si3Аl4O12, или же, наконец, сочетанием всех этих составов, как слагающих. Первый шаг был сделан, но все же вопрос о том, какие именно сочетания представлены в слюдах, оставался до самого последнего времени несдвинувшимся с мертвой точки, и мы имели пред собой несколько сот отдельных анализов, как бы безформенную груду, из которой никаких определенных выводов сделать казалось невозможным; а между тем именно в этой груде скрылись труды даже первоклассных корифеев химического анализа, привлеченных именно трудностью вопроса и очевидно имевших надежду преодолеть все трудности дела.
Однако, если это не удалось даже корифеям, то это произошло оттого, что трудности, если и имеются, то не там, где их ожидали. Весь расчет сводился на особую точность анализа, а на деле нужно было наглядно представить полученные результаты; об этом же не возникало и мысли, потому что заранее предполагалось, что если анализ будет достаточно точен, то сам собою вытечет и результат в виде отношения состава окислов в целых числах. Применение способов наглядного изображения результатов показало, что это не так.
И вот, достаточно было найти способ изобразить результат каждого отдельного анализа минерала в виде определенной точки в пространстве, чтобы вместо безформенной груды анализов получить скопление точек в пределах одного треугольника с точно определенными тремя вершинами, хотя бы самих вершин в состав результатов анализа и не попало. Этого результата вполне достаточно, чтобы видеть, что все слюды слагаются из изоморфного (то есть из кристаллически одинаковой формы частей, могущих в любой пропорции замещать друг друга) смешения трех минералов более или менее строго определенного состава, получаемых путем попарной группировки для основных групп: Si(K,H)4O4, SiMg2O4, Si3Al4O12. Неопределенность сохраняется только в возможности частичной замены одних окислов другими, равнозначными (одноатомных одноатомными же и т. д.).
Если для выражения пропорции, в которую входят эти слюдослагающие три минерала, мы на первом месте поставим число, соответствующее количеству одноатомных, на втором число, соответствующее количеству двухатомных окислов и т. д., то, рассматривая полученное изображение, мы найдем для них три следующие отношения. 2):
1) — (1011), 2) — (4403) и 3) — (0445). Вот каковы те три минерала, из произвольного смешения которых происходят все остальные слюды. И что особенно замечательно, что отношения этих целых чисел не есть какие то приближенные, а, можно сказать, есть отношения математически точные, несмотря на то, что в состав опытного материала, положенного в основание, нет ни одного совершенно точного примера, и каждый из них, взятый в отдельности, представляет отклонение в ту или другую сторону, в меньшей или большей степени, а не меньше половины материала представляет уклонение настолько значительное, что им лучше даже и не пользоваться; более же внимательное рассмотрение раскрывает все преимущество результатов, полученных лучшими знатоками анализа и даже дает основания для суждения об относительной оценке приложивших сюда свои силы высших авторитетов.
Я имею основание опасаться даже, что возможность получения столь неожиданных результатов от применения таких элементарных приемов, как простая наглядность в изображении сырого материала, может вызвать недоумение, что получение таких определенных и притом совершенно точных выводов путем, так сказать, простого упорядочения в расположении имеющегося материала может показаться почти невероятным и потому, думается, что любознательность невольно подтолкнет познакомиться с теми простыми техническими приемами, посредством которых результат оказался достигнутым и химический состав слюд, как таковых, сразу стал вполне ясным.
Вот почему, в дополнение к предыдущему изложению, я вкратце остановлюсь и на практике осуществления этих приемов.
Применение их по четырем целым числам, выражающим отношения четырех разрядов окислов, должно дать в пространстве точку, как выражение отдельного анализа. С математической точки зрения такие отношения четырех чисел представляет не четыре, а только три данные, так как ни одно из этих чисел не имеет само по себе абсолютного значения, а таковое принадлежит лишь его отношению к другим; если я напишу напр. это отношение в виде
| (abcd) или в виде | ( | 1 | b | c | d | ), | ||
| a | a | a |
то только в форме внешнего выражения представляется нечто различное, а по существу это одно и то же. Словом, мы не получим никакого различия в существе дела, если все четыре числа помножим или разделим на одно и то же. В частности, мы можем принять эти числа и за выразителей процентного содержания, то есть придать им такое значение, чтобы их сумма стала равною ста.
Но если мы сделаем это, то зависимость каждого числа от всех остальных станет еще более очевидною: чтобы знать все четыре числа, нам достаточно иметь только три из них, потому что четвертое число само собою получается вычитанием из ста суммы трех остальных. И если мы получим точку только по трем из этих чисел, то в сущности ее можно считать построенною и по всем четырем, потому что по положению точки мы будем знать и четвертое число.
А по трем числам действительно легко построить определенную точку в пространстве. Для этого достаточно взять произвольно некоторую точку (начало координат) и провести из нее три взаимные перпендикуляра (оси координат) и отметить их числами в определенном порядке как первую, вторую и третью ось. По первой оси отложим, напр. длину, соответствующую первому числу; из полученной точки представим себе движение, параллельное второй оси, и на проходимой линии отложим длину, соответствующую второму числу, и, наконец, из достигнутой нами при этом движении точки проведем параллельную третьей оси, и на ней отложим длину, соответствующую третьему числу. В результате мы пришли к совершенно определенной точке в пространстве, ясно выражающей своим положением все четыре данные числа, которые мы и можем восстановить по этому положению.

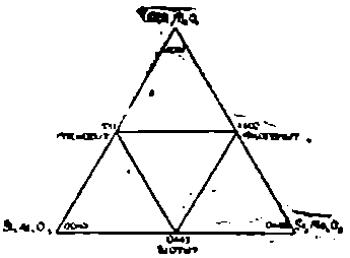
Этим способом, соответственно каждому данному анализу, мы получим одну точку. И каково же будет наше удовлетворение, когда мы заметим, что все точки с достаточною удовлетворительностью укладываются в одной наклонной плоскости в том внутреннем треугольнике, который схематически изображен на приложенной фигуре. Мало того, точки достаточно густо расположенные в определенных пределах, совершенно не выходят из этих пределов, а сами пределы превосходно очерчиваются в виде трех прямых, попарно пересекающихся в точках, находящихся на особых плоскостях, а именно плоскостях, в которых попарно находятся взятые нами оси (плоскостях координат). Правда, все это осуществляется не с совершенной точностью; ясно намечается, что отдельные точки то выше, то ниже плоскости, а некоторые точки даже несколько выходят за пределы сторон упомянутого треугольника, но так незначительно, что достаточно знать технику химического анализа, чтобы понять, что иначе и быть не может.
На каком же основании мы по таким неточным результатам отдельных отложений можем утверждать о совершенной точности конечных результатов, и в частности, что приведенные именно выше числа выражают состав слагающих слюд с совершенною точностью.
Чтобы понять правильность такого утверждения, достаточно вспомнить о некоторых законах природы, которым никто не отказывал в совершенной точности.
Ближе всего здесь вспомнить о законе Дальтона кратных отношений в химических частицах. Открытый на обширном опытном материале, он имел своим логическим последствием вывод понятия об атомах и об определенном порядке сцепления этих атомов — частице, — при котором возможна только связь в отношении целых чисел. И то, что могло еще сто лет тому назад иметь налет гипотетичности, теперь совершенно свободно от такого налета, так как дело дошло до ближайшего пространственного изучения этой связи.
Ясно, что если вообще по трем, даже самым точно-определенным точкам мы получаем на деле плоскость, которая не совершенно точно пересекает проведенные нами оси в точках (4001), (0201) и (0043), а только весьма приближенно, то совершенно ясно, что эта приближенность не случайная и что замена случайно получаемых точек, очень близких к ним, именно этими точками, есть логическое следствие закона кратных отношений. В свою очередь, эти точки легко получаются с совершенною точностью: это те самые точки (уже упомянутые выше), в которых плоскость точек, выражающих ортосиликаты, пересекает оси координат. Таким образом вновь подтверждается, что все слюды представляют собою ортосиликаты.
В заключение упомяну, что между этими тремя числами, относящимся к вершинам полученного трехугольника, имеется весьма простое отношение, а именно: числа (0445) слагаются из чисел
| (0201) и (0043) | 0 | 0 | 4 | 3 | , |
| + | + | + | + | ||
| 0 | 4 | 0 | 2 |
числа (1011) слагаются из
| (0043) и (4001) | 4 | 0 | 0 | 1 | , |
| + | + | + | + | ||
| 0 | 0 | 4 | 3 |
а числа (4403) слагаются из
| (0201) и (4001) | 0 | 4 | 0 | 2 | . |
| + | + | + | + | ||
| 4 | 0 | 0 | 1 |
Это соотношение при обсуждении вопроса становится понятным, но на этом уже не будем останавливаться.
Конечно, нет науки без сырого материала. Но сырой материал не необходимо черпается из научных лабораторий, а может заимствоваться и из случайных наблюдений, извлекаться из неисчерпаемого источника явлений и предметов природы, равно как и из людского обихода. Спрашивается, что представлял бы из себя весь этот материал, какого бы происхождения он ни был, если бы он не подвергался специализированному добавочному научному труду?

1) Желающих ознакомиться более серьезно с поднимаемым в этой статье вопросом отсылаю к ряду статей Е. С. Федорова в Известиях Академии Наук за 1919 г. (№ 2). Прим. ред. (стр. 243.)
2) Также и вышеприведенные формулы Si(К, Н)4O4, SiMg2O4 и Si3Al4O12 мы можем соответственно заменить выражениями (4001), (0201) и (0043). (стр. 248.)