"Природа", №01-02, 1926 год, стр. 35-52.
1. В 1672 году Ньютон, пропустив через стеклянную призму солнечный луч, проходящий сквозь отверстие в оконном ставне, получил на противоположной стене полосу, окрашенную в яркие цвета: красный, желтый, зеленый, голубой и фиолетовый. Эту полосу он назвал спектром. Ньютон считал, что свет состоит из маленьких частиц, вылетающих по всем направлениям из светящегося тела. Однако, эта теория не могла объяснить, наблюденные впервые Гримальди, явления диффракции (огибание преград) и интерференции (сложение лучей). Эти явления нашли свое естественное объяснение в волновой теории Гюйгенса, развитой впоследствии Томасом Юнгом и Френелем.
Явления интерференции и диффракции позволили определить длину световой волны В 1821 году Фраунгофер показал, что если на стеклянную пластинку нанести большое число равноотстоящих непрозрачных штрихов, то такая "решетка" (диффракционная решетка) дает спектр и позволяет с большой точностью определять длины световых волн. Длина световой волны λ величина весьма малая; она равна нескольким стотысячным долям сантиметра. Наименьшей длиной волны, именно около 0,4 µ, обладают фиолетовые лучи, наибольшей (0,76 µ) — красные.
При исследовании спектра естественно возникли вопросы: почему спектр прекращается у красного и фиолетового конца? Существуют ли длины волн большие 0,76 µ и меньшие 0,4 µ? И действительно еще в конце 18-го столетия было открыто, что спектр простирается далеко, как за красную, так и за фиолетовую область. В 1877 году химик Шееле нашел, что хлористое серебро краснеет, если его поместить за фиолетовым концом спектра. В 1800 году Гершель по нагреванию весьма малого термометра обнаружил существование лучей и за красным концом спектра. Таким образом были открыты невидимые части спектра — инфракрасная и ультрафиолетовая, как их принято называть. То, что о природе этих лучей в свое время делались различные гипотезы, имеет теперь лишь историческое значение. С развитием волновой теории было показано, что эти новые лучи отличаются от видимых только длиной волны. Инфракрасные лучи имеют длины волн большие, чем видимые, ультрафиолетовые — меньшие.
Когда была изобретена фотография, оказалось, что ультрафиолетовые лучи сильно действуют на фотографическую пластинку, что сразу облегчило изучение этой новой области. Первый, тшательно изучавший ультрафиолетовые спектры различных элементов, был французский физик Маскар. Ему и несколько позже Корню удалось промерить спектр алюминия вплоть до 0,1852 µ, или, что то же самое, 1852 А 1). В последующие годы большое число работ, которых мы коснемся ниже, позволили продвинуться в ультрафиолетовую область до λ = 1216 А (спектр водорода).
Еще в начале 19-го столетия было установлено, что раскаленные пары и газы дают спектры, состоящие из отдельных ярких линий на темном фоне. Такие спектры были названы линейчатыми. Газ, дающий такой линейчатый спектр, испускает волны лишь вполне определенных длин. Каждый химический элемент имеет свой собственный характерный для него линейчатый спектр. Отсюда атом каждого элемента должен представлять собой сложный механизм, способный испускать свет вполне определенных длин волн. В 1873 году Максвелл показал, что световые волны суть весьма короткие электромагнитные волны; они отличаются от электрических волн, открытых Герцем, лишь своей малой длиной. Таким образом каждый атом должен представлять собой некоторый электрический вибратор. Теория Максвелла, объединив столь разнородные яоления, как свет и электрические лучи Герца — позволила говорить об общей шкале электромагнитных волн.
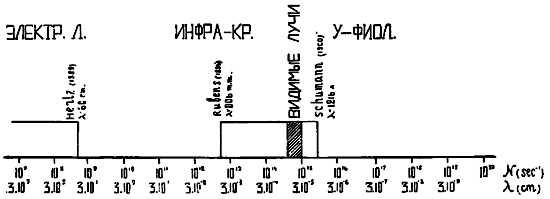
Мы можем иметь сколь угодно медленные электрические колебания, а следовательно и сколь угодно длинные волны. Наиболее же короткие, из известных в конце прошлого столетия, волны Герца, имели длину около 60 см. На чертеже 1-ом изображена шкала электромагнитных волн, относящаяся приблизительно к 1900 году. Для удобства вдоль горизонтальной линии отложены логарифмы частот; там же помечены и длины волн. Заштрихованный прямоугольник относится к видимой части спектра. Налево идут инфракрасные лучи, известные в то время до λ = 0,06 mm. Направо — ультрафиолетовые, пределом которых является, уже упомянутая выше, линия водорода λ = 1216 А.

Бросив взгляд на чертеж, мы видим, что шкала имеет с одной стороны естественную границу: бесконечно-длинные волны, т.-е. статическое поле постоянных зарядов. Также естественно возникает задача о заполнении еще неисследованного промежутка между крайними электрическими и инфракрасными лучами. Вопрос же о "короткой" границе шкалы остается открытым.
Насколько далеко простираются ультрафиолетовые лучи? Нет ли нового сорта электромагнитных волн значительно более коротких, чем лучи видимые и ультрафиолетовые?
И, действительно, в 1895 году Рентген открыл новый вид лучей. Это открытие тесно связано с установлением атомного строения электричества. Целым рядом исследователей было показано, что нельзя получить сколь угодно малый электрический заряд. Он не может быть меньше некоторого числа е = 1,59·10—20 в электромагнитных единицах. Также невозможен заряд в нецелое число е. Эта элементарная частица электричества обладает массой и всегда несет отрицательный заряд. Ее назвали электроном. Кроме указанного заряда е, электрон характеризуется отношением заряда к массе e/m = 1, 769·107 (эл.-магн. ед.). Положительный заряд всегда связан с материей.
Рентген пропускал сквозь тщательно откаченную трубку поток свободных электронов. Он заметил, что из того места, куда попадают электроны, исходят какие-то новые лучи, обладающие рядом замечательных свойств. Природа этих лучей долгое время оставалась неизвестной. Они не обнаруживали явлений диффракции, откуда следовало,что если они и являются электромагнитными волнами, то чрезвычайно малой длины; по вычислениям Зоммерфельда их длина не должна была превышать 10—8 см., т.-е. 1 А. Наконец, в 1912 году Лауэ пришла счастливая мысль воспользоваться в качестве диффракционной решетки для рентгеновых лучей кристаллами. Кристаллы характеризуются строгим пространственным распределением атомов, из которых они состоят. Они представляют собой весьма тонкие пространственные решетки. Из теоретических соображений можно было показать, что такая пространственная решетка должна действовать на достаточно короткие волны, как обычная диффракционная решетка действует на оптические длины волн. Для коротких же длин волн обычная решетка слишком груба. И действительно, исследуя рентгеновы лучи, проходящие сквозь кристаллы и отраженные от них, можно было обнаружить диффракционную картину. Дальнейшие опыты позволили получить и сфотографировать настоящие рентгеновы спектры.
Если в рентгеновой трубке антикатодом (т.-е. тем местом, куда попадает пучок электронов) служит какой-либо элемент, то испускаемые рентгеновы лучи дают определенный линейчатый спектр. Таким образом каждый химический элемент, кроме оптического, имеет еще характеристический рентгенов спектр. Мозелей, в 1913 году, первый изучил характеристический рентгенов спектр ряда элементов: Са, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn и промерил их длины волн, которые заключались от 3,368 А до 1,306 А, т.-е. были порядка 1—3 А. Таким образом на нашей шкале электромагнитных волн прибавляется новая область, что и отмечено на чертеже 2-м.
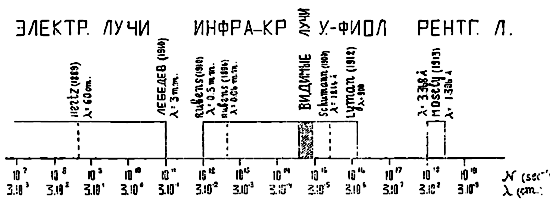
Чертеж 2-ой ставит новую задачу: заполнить промежуток между рентгеновыми и ультрафиолетовыми лучами, а вместе с тем перед нами встает и более широкий вопрос о взаимоотношении между рентгеновыми и видимыми спектрами.
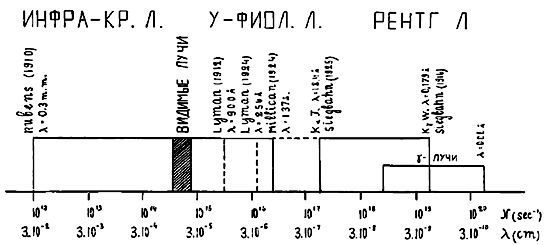
2. Если природа предоставила нам в кристаллах готовые диффракционные решетки для исследования рентгеновых лучей, то она же и поставила предел этим исследованиям. Для длин волн в 15—20 А кристаллы являются решетками уже чересчур тонкими. В настоящее время из промеренных длин волн обладает наибольшей длиной так называемая линия Кα фтора λ = 18,37 А; в то время как наименьшей длиной волны — линия Кψ вольфрама λ = 0,179 А; еще более короткими длинами волн обладают γ-лучи радиоактивных веществ, которые также являются электромагнитными волнами. На чертеже 3-м, который представляет собой часть шкалы электромагнитных волн, изображена вся исследованная в настоящее время область рентгеновых спектров, а также отмечена область занимаемая γ-лучами.
Отсутствие кристаллов с достаточно большой постоянной решетки не позволяет нам распространить рентгеновы спектры дальше, чем до 16—20 А. Остается делать попытки подойти к неисследованной области со стороны ультрафиолетовых лучей. Мы уже указывали, что Маскар и Корню фотографировали с помощью диффракционной решетки ультрафиолетовые спектры различных элементов. Им удалось продвинуться приблизительно до λ = 1800 А. Дальнейшая работа затрудняется тем, что почти все вещества становятся непрозрачными для таких коротких волн (для очень коротких, рентгеновых лучей, они опять прозрачны). Стекло поглощает приблизительно с λ = 3500 А. Маскар и Корню работали с кварцевыми линзами. Самым прозрачным из всех известных твердых веществ является флюорит. Короткие ультрафиолетовые лучи поглощаются не только линзами и призмами, но и самим воздухом. Приходится весь спектроскоп делать коротким и располагать источник света как можно ближе к щели, чтобы по возможности уменьшить путь лучей в воздухе. Но начиная с 1800 А воздух уже настолько непрозрачен, что даже самый небольшой его слой делает работу невозможной.
Шуман, чтобы избегнуть поглощения в воздухе, построил вакуум-спектрограф. Остов его спектрографа закрывался герметически и из него выкачивался воздух. Линзы и призмы были из флюорита. Источник света ставился вплотную к щели. Однако, Шуману пришлось преодолеть еще одно препятствие: оказалось, обычные фотографические пластинки не пригодны для снимков в этой области. Дело в том, что слой желатины толщиной всего в 0,01 mm. уже совершенно поглощает лучи начиная с 2200 А. Таким образом ультрафиолетовые лучи не могут подействовать на чувствительную эммульсию пластинки и вызвать фотографический процесс. Шуману удалось получить пластинки, на которые бромистое серебро наносилось без посредства желатины. Это позволило ему сразу значительно продвинуться вперед. Однако, Шуман работал с призмой, а потому не мог точно определить длины волн. Отклонение луча в призме зависит от коэффициента преломления n, а уже только этот последний зависит от длины волны. Зависимость же коэффициента преломления флюорита от длины волны в далекой ультрафиолетовой области, конечно, не могла быть известна. Шуманэкстраполировал формулы пригодные для видимой части спектра и на основании этого предполагал,что дошел до λ = 1000 А. В более старых учебниках это число и указывается, как предел "Шумановской области". На самом деле, как впоследствии показал Лейман, флюорит прозрачен лишь до 1200 А и экстраполяция, примененная Шуманом, не верна. Крайняя водородная линия, с которой имел дело Шуман, имеет λ = 1216 А, что и помечено на чертежах 1-м и 2-м.
Все дальнейшее исследование крайней ультрафиолетовой области принадлежит американским физикам Лейману и Милликэну. Чтобы иметь возможность действительно мерить короткие длины волн, Лейман решил воспользоваться решеткой, именно вогнутой решеткой, которая не требует линз. Решетки бывают прозрачные и отражательные. Еще в 1882 году Роланд показал, что если в отражательной решетке штрихи наносить не на плоское металлическое зеркало, как обычно, а на цилиндрическое вогнутое, то такая решетка обладает фокусирующим действием и чтобы с помощью ее получить действительное изображение спектра вовсе не нужно линз. Существуют сплавы, являющиеся хорошими зеркалами и для далеких ультрафиолетовых областей; это позволяет получить вогнутые отражательные решетки, пригодные для работы с весьма короткими лучами. Такой решеткой и воспользовался Лейман. Из всего кожуха, в котором располагались решетка, фотографическая кассета и другие части спектрографа, выкачивался воздух. Таким образом в спектрографе Леймана можно было избегнуть всякого поглощения. Работа с герметически-закрытым вакуум-спектрографом, да еще "в темную" (ведь ультрафиолетовых лучей видеть нельзя), представляет большие трудности. Но трудности встречаются не только чисто экспериментального характера, но и более принципиального. Прежде всего решетка: те длины волн, с которыми имел дело Лейман (до 500 А), приблизительно в 10 раз короче волн видимого спектра (зеленый свет имеет λ = 5000 А). В соответствии с этим и всякая неправильность в решетке сказывается значительно сильнее. Чтобы получить такие же результаты, как и в видимой области, нужно изготовить решетку в десять раз лучшую, что технически невыполнимо. Во-вторых, всякая решетка, как известно, дает не одно, а несколько изображений одного и того же спектра, как говорят, спектры различных порядков. Каждый последующий спектр более растянут, чем предыдущий и спектры частью накладываются друг на друга. Именно, на длину волны λ1, в спектре первого порядка, накладывается длина волны λ2 = ½λ1 второго порядка, λ3 = ⅓λ1 третьего и т. д. В видимой области это фактически не мешает, потому что на длину волны, соответствующую красному краю, λ = 7600 А первого порядка накладывается λ = 3800 А второго порядка, т.-е. ультрафиолетовая область, не действующая на глаз. Но если мы возьмем λ = 1500 А первого порядка, то на нее наложатся λ = 750 А второго порядка, λ = 500 А третьего и т. д. — области, которые все одновременно окажутся сфотографированными и будут мешать друг другу.
Наконец, самое существенное затруднение — это источник света. Его нельзя отделить от спектроскопа окошком, так как для коротких лучей не существует никаких прозрачных окошек. Всякий же источник света, будь то дуга, искра, или гейслерова трубка, требует определенного и не слишком малого давления окружающего газа. Всякий же газ внутри спектрографа нежелателен, потому что он будет поглощать. Лейман, он работал с водородом и гелием, приклеивал гейслерову трубку непосредственно к щели. Весь прибор наполнялся сухим газом при таком давлении, чтобы в трубке мог происходить разряд. Никакого окошка не было, но зато газ, хотя и при малом давлении, находился в приборе и сильно поглощал испускаемые лучи. В водороде Лейман наблюдал целый ряд, или как принято выражаться серию, линий, крайняя из которых (со стороны больших длин волн) была уже наблюденная Шуманом линия λ = 1216 А. Так как работа велась с решеткой, то здесь в определении длин волн исключалась ошибка, аналогичная ошибке Шумана. Кроме водорода Лейман наблюдал линии гелия вплоть до λ = 900 А, что и отмечено на чертежах 2-м и 3-м.
В 1919 году за исследование крайнего ультрафиолетового спектра взялся Милликэн, один из самых блестящих экспериментаторов нашего времени. Он пользовался прибором, сходным с прибором Леймана. Но, во-первых, он имел в своем распоряжении отличные вогнутые решетки, изготовленные в лаборатории Вуда. Эти решетки отличались не только замечательной правильностью, но и способностью давать спектр какого-либо одного порядка несравненно более яркий, чем спектры остальных порядков. Это в значительной мере уменьшило неприятности от наложения спектров друг на друга. Во-вторых, Милликэн сделал важное открытие: он нашел, что и в лучшем вакууме может быть получена искра, если располагать электроды очень близко друг от друга (доли mm) и прикладывать к ним очень высокие вольты (сотни тысяч). Таким образом он мог удалить весь газ из спектроскопа и вовсе отделаться от поглощения. В своих первых же работах Милликэн продвинулся значительно вперед: он дошел до λ = 200 А. За последующие годы он исследовал крайние ультрафиолетовые спектры большого числа элементов, преимущественно двух первых строк таблицы Менделеева. В настоящее время пределом достигнутой длины волны является линия Al, λ = 136,6 А. О большом теоретическом значении этих работ мы скажем ниже.
Одновременно и Лейман достиг новых успехов. Он употреблял гейслерову трубку особого устройства, в которой свечение наблюдалось вдоль узкого капилляра. Этим узким капилляром трубка и была приклеена к щели. Таким образом газ мог лишь с трудом просачиваться внутрь спектрографа и оттуда сейчас же убирался мощными насосами. В трубку же, чтобы не менялся режим ее сечения, все время поступал новый газ. Лейман наблюдал спектр гелия до λ = 256 А.
3. В конце 1-го параграфа мы поставили две задачи: одну, если можно так выразиться, более спортивного характера, заполнить промежуток между ультрафиолетовыми и рентгеновыми лучами; другую — более теоретическую: выяснить взаимоотношение этих двух спектральных областей. Мы видели, задача о заполнении неисследованного промежутка в значительной степени продвинута вперед. В настоящее время, с одной стороны, сфотографированы и промерены ультрафиолетовые лучи в 20 раз более короткие, чем видимые, а с другой, получены рентгеновы линии длиной в полтора десятка ангстрем. На самом деле, несколько косвенным путем (методом, основанном на фото-электрическом эффекте) выхвачен ряд точек и в промежуточной области, что отмечено пунктиром, на нашем чертеже 3. Во всяком случае, для теоретических построений материала достаточно.
И, действительно, теория Бора пролила свет, как на природу оптических, так и рентгеновых спектров. Бор высказал свою теорию в 1913 году. В настоящее время ее значение огромно; она проникла решительно во все отделы физики, а частью в химию и астрономию; подавляющее число вновь появляющихся физических работ так или иначе связано с ней. При первом знакомстве теория Бора может казаться чрезвычайно искусственной. На самом деле, она не только a posteriori оправдывается большим числом наблюдений, но и в значительной степени принудительно навязывается нам фактическими данными.
Электромагнитная теория света и существование линейчатых спектров заставили нас считать атом за сложную электрическую систему. Электронная теория, установив реальное существование элементарной частицы отрицательного электричества, электрона, в 1800 раз более легкого, чем атом, указала нам, где искать те кирпичи, из которых построены атомы.
Замечательные работы Резерфорда над прохождением α-частиц, выбрасываемых радиоактивными веществами сквозь материю, привели к взгляду, что атомы построены подобно солнечной системе: в центре весьма малое, положительно-заряженное ядро, в котором сосредоточена почти вся масса атома; кругом, сравнительно на больших расстояниях, подобно планетам, вращающиеся электроны. Число электронов в атоме данного элемента равно порядковому номеру Z этого элемента в периодической системе Менделеева, т.-е. для водорода равно 1-му, для гелия 2-м, для берилия 3-м и т. д. Заряд ядра E = +Ze, где е — заряд электрона. Однако, такая система неустойчива. По классической электродинамике электрон, вращающийся вокруг ядра, должен непрерывно испускать свет, а следовательно испускать и энергию, что в результате приведет к катастрофе: электрон упадет на ядро. На самом же деле атомы чрезвычайно устойчивы. Бор предположил, что вопреки классической электродинамике и в согласии с фактическими данными, движение электронов по орбитам вокруг ядра устойчиво; при этом, опять таки в противоречии с классическими представлениями, электроны не лучеиспускают.
Что касается процесса лучеиспускания, то здесь также имеются обстоятельства, подсказывающие решение. Атом должен испускать линейчатый спектр. Линии же в спектрах располагаются не беспорядочно, но по строгим, так называемым сериальным, законам. Именно, еще в 1885 году Бальмер показал, что частоты всех тогда известных линий водорода выражаются формулой:
| ν = N | ( | 1 | — | 1 | ) | ....... (1) |
| 2² | n² |
где N постоянная, равная 1,097·105, а n = 3, 4, 5, 6, ..., т.-е. придавая n указанный ряд значений последовательных целых чисел, мы получим частоты, а следовательно и длины волн, отдельных линий, начиная с крайней красной. Эта формула дает с величайшей точностью длины волн всех 29-ти тогда известных водородных линий. Впоследствии Ридберг показал, что у многих элементов могут быть выделены такие группы, или, как принято их называть, серии линий, что внутри каждой серии частоты линий охватываются формулой, аналогичной формуле Бальмера.
С другой стороны, еще за 13 лет до Бора, немецкий физик Планк показал, что для того чтобы могло существовать тепловое равновесие (а в природе оно осуществляется) и чтобы объяснить фактически наблюдаемое распределение энергии в сплошном спектре, нужно предположить, что атомы испускают энергию не непрерывно, но порциями, квантами, величина которых зависит от частоты испускаемого излучения ν.
где h постоянная, равная 6,55·1023 erg/sec.
Соединяя все сказанное выше в одно, Бор высказал следующую теорию строения атомов: атомы, согласно с Резерфордом, построены наподобие солнечной системы. Движение электронов, вопреки классической электродинамике, устойчиво и происходит без излучения. Однако, устойчивы не все механически возможные орбиты, а только некоторые, удовлетворяющие определенным условиям (квантовым условиям). Только эти последние орбиты фактически и осуществляются. Они называются стационарными. Энергия атома, соответствующая движению электрона по одной из таких орбит, может быть вычислена. По второй гипотезе Бора, лучеиспускание происходит при переходе атома из одного стационарного состояния в другое. Механизм этого излучения остается неизвестным. Если мы обозначим энергию начального состояния через W', а конечного через W", то во время верехода атом испустит разность энергий ΔW = W' — W". В согласии с Планком, Бор полагает, что частота ν этой испущенной порции лучистой энергии определяется соотношением:
откуда, подставив вместо ΔW его значение W' — W", получим:
| ν = | W' | — | W" | ....... (2) |
| h | h |
"правило частот" Бора, которое, не касаясь механизма самого излучения, позволяет по энергиям атома в различных стационарных состояниях определить испускаемые им частоты, т.-е. определить его спектр. В случае простейшего атома, состоящего из ядра с зарядом Е и одного электрона, задача может быть решена до конца. Расчет дает, что такой атом должен испускать спектр, состоящий из большого числа линий, частоты которых охватываются следующей формулой:
| ν = N | ( | E | ) | 2 | {( | 1 | ) | — | ( | 1 | )} | ....... (3) |
| e | m² | n² |
где N некоторая постоянная, E/e — отношение заряда ядра к заряду электрона: m и n — два целых числа, именно n — квантовое число, характеризующее то стационарное состояние, в котором атом находился до акта лучеиспускания, a m — квантовое число конечного стационарного состояния. Для водорода Е = е, т.-е. E/e = 1, что упрощает формулу (3). Кроме того, полагая, что атом переходит во 2-ое стационарное состояние, т.-е. что m = 2, получим:
| ν = N | ( | 1 | — | 1 | ) |
| 2² | n² |
выражение, совпадающее с формулой Бальмера (1). Мало того, по теории Бора число N может быть вычислено, так как оно выражается через заряд и массу электрона и постоянную Планка h. Для N получается значение N = 1,09·105, в то время как в эмпирически установленной формуле Бальмера N равнялось N = 1,097·105 — совпадание, как видно, полное. Таким образом, теория Бора позволяет по измерениям, не имеющим ничего общего со спектром водорода, точно предвычислить длины волн его линий.
Серия Бальмера испускается при переходе атома из более высоких стационарных состояний во 2-ое состояние. Можно поставить вопрос, что будет, если атом станет переходить в 1-ое стационарное состояние? Теория дает, что при этом должна испуститься частота:
| ν = N | ( | 1 | — | 1 | ) | ....... (4) |
| 1² | n² |
или в переводе на длины волн, линии:
λ = 1215,68 А
λ = 1025,73 А
λ = 972,55 А и т. д.
Как мы уже указывали, Лейман наблюдал ряд ультрафиолетовых линий водорода, первая из которых имела длину волны 1216 А, а две других λ = 1026,0 и λ = 972,7 А, что вполне совпадает с теоретическими. Интересно отметить, что существование этих линий было установлено Лейманом уже после создания теории Бора, так что в этом случае Бор предсказал новый, впоследствии оправдавшийся факт.
Если мы перейдем к следующему в таблице Менделеева элементу, к гелию, то он состоит из ядра и двух электронов. Здесь механическая задача о движении электронов не может быть решена, а вместе с тем не может быть предвычислен и спектр гелия. Но если мы станем рассматривать гелий, от которого отнят один электрон (ионизованный гелий), такие ионизованные атомы всегда встречаются при наличии сильного электрического разряда, то он будет подобен водороду, с той только разницей, что здесь заряд ядра Е = +2е, откуда по формуле (3) частоты, испускаемые при переходе в первое стационарное состояние, представятся формулой:
| ν = 4N | ( | 1 | — | 1 | ) |
| 1² | n² |
а испускаемые при переходе во второе стационарное состояние:
| ν = 4N | ( | 1 | — | 1 | ) |
| 2² | n² |
Обе формулы совершенно аналогичны формулам Леймановской и Бальмеровской сериям (4) и (1) водорода, только постоянная N заменена через 4N, что происходит вследствие вдвое большего, по отношению к водороду, заряда атомного ядра. Благодаря этому множителю 4 частоты увеличиваются в 4 раза и весь спектр сдвигается далеко в ультрафиолетовую часть. Ниже мы увидим, что спектры всех ионизованных атомов всегда сдвигаются в сторону коротких длин волн. На самом деле, Лейман, пропуская очень мощный разряд через гейслерову трубку с гелием, мог наблюдать ряд далеких ультрафиолетовых линий, длины волн которых, как это видно из прилагаемой таблицы, совпали с теоретическими:
|
|
||||||||||||||||||||
| n | λ набл. | λ вычисл. | n | λ набл. | λ вычисл. | ||||||||||||||||
| 3 | 1640,4 | 1640,49 | 2 | 303,6 | 303,7 | ||||||||||||||||
| 4 | 1215,2 | 1215,18 | 3 | 256,3 | 256,25 | ||||||||||||||||
| 5 | 1085,2 | 1084,98 | |||||||||||||||||||
Перейдем к более сложным атомам. Мы уже указывали: число электронов в атоме равно его порядковому номеру в периодической системе. Таким образом у атома натрия 11 электронов, у цинка — 30, у урана — 92. По современным представлениям электроны в атомах располагаются на различных расстояниях от ядра, определенными группами, или, как принято выражаться, составляя определенные электронные оболочки. Каждая оболочка характеризуется своим квантовым числом. По Бору оптические спектры испускаются наиболее внешними электронами. Для сложных атомов энергия электронов не может быть точно вычислена, но можно указать, что частоты испускаемых линий будут выражаться формулой, аналогичной эмпирически установленной формуле Ридберга.
Рентгеновские лучи излучаются внутренними электронами. В самом деле, рассмотрим наиболее внутренний электрон какого-либо атома. Если число внешних электронов велико, то они расположатся более или менее симметрично и их воздействия на внутренний электрон в значительной степени уничтожаются. Таким образом самый внутренний электрон находится в условиях близких к условиям единственного водородного электрона. Только здесь притяжение со стороны ядра больше, благодаря его большему заряду E = +Ze, где Z порядковый номер данного элемента. Если бы мы имели систему, состоящую только из ядра с зарядом E = +Ze и одного электрона, то, как мы уже указывали, частоты линий, испускаемых таким атомом, выражались бы формулой (3). На самом деле внешние электроны несколько изменяют условия, они как бы уменьшают заряд ядра от значения +Ze до значения +(Z — s)е, где s небольшое число. В соответствии с этим несколько изменится и испускаемый спектр. Если для самого внутреннего электрона осуществимы две стационарные орбиты, характеризуемые квантовыми числами К = 1 и К = 2, то, переходя с одной из этих орбит на другую, он испустит частоту:
| ν = N(Z — s)2 | ( | 1 | — | 1 | ) | ....... (5) |
| 1² | 2² |
Благодаря множителю (Z — s)2 частота ν для электронов с большим порядковым номером Z весьма велика, а, следовательно, длина волны весьма мала, именно она того же порядка, как длина волн рентгеновых лучей. Переходы внутренних электронов могут произойти под влиянием очень сильного толчка извне, который реализируется в рентгеновых трубках ввиде удара со стороны катодного пучка.
Промеры Мозелея показали, что частоты определенных рентгеновых линий (так называемых К-линий) всех элементов в точности выражаются формулой (5), если положить s = 1. Та же формула при s = 0 и Z = 1 и Z = 2 совпадает с формулами ультрафиолетовых серий водорода и гелия.
Остальные рентгеновы линии (их длина волны больше, чем длина волны К-линий) возникают при перескоках в последующих, считая от самой внутренней, электронных оболочках. Наоборот, если мы исходя из оптических спектров, испускаемых самым внешним электроном, станем ионизировать атом, т.-е. отнимать от него один за другим электроны, то мы тем самым будем переходить к более внутренним оболочкам. Так как в более внутренних оболочках электроны двигаются под влиянием большего притяжения со стороны ядра, то постоянная N в сериальных формулах умножится на z12, где Z' = 2 в случае ординарной ионизации, Z'= 3 в случае двойной и т. д. Это вызовет увеличение частоты ν, т.-е. смещение спектра в ультрафиолетовую часть. Спектры таких ионизованных атомов и наблюдал Милликэн; ионизация происходила благодаря мощному разряду в его искре; спектры располагались в крайней ультрафиолетовой части.
Таким образом принципиальной разницы между оптическими и рентгеновыми спектрами не существует. Первые испускаются внешними электронами, вторые внутренними. Для легких элементов с малым порядковым номером Z, с малым числом электронов, разница, вообще, исчезает. Ультрафиолетовые Леймановские серии водорода и ионизованного гелия одновременно являются рентгеновыми К-сериями. Далекие ультрафиолетовые серии легких элементов, полученные Милликэном — аналогичны рентгеновым L- и М-сериям тяжелых элементов. Вся область от видимого до крайнего рентгенова спектра однородна и должна быть сплошь заполнена. Работы в далекой ультрафиолетовой части перекинули действительный мост между двумя областями, показав их внутреннее сродство. Вместе с тем эти работы еще раз привели нас к вопросу о строении атомов, а следовательно и строении и сущности материи. Таким образом, может быть нигде, как в физике, оправдывается пословица, что все дороги ведут в Рим.
1) Ангстрем, употребляемая в спектроскопии единица длины, равная 1·10—6 см. = 1·10—4 µ; названа в честь шведского физика Ангстрема.
(стр. 36.)