"CQ-SKW", №20, октябрь, 1930 год, стр. 170-171
инж. З. ГИНЗБУРГ
Мы разобрали случай, когда нужно построить дросселя, причем вам задана величина самоиндукции, которой дроссель должен обладать, а также и нормальная сила тока, которая через него проходит.
Рассмотрим теперь второй поставленный вами вопрос, а именно: тот случай, когда дроссель уже имеется, число его витков, сечение провода (или его диаметр) известны, но мы не знаем ни самоиндукции, ни величины воздушного зазора, с которым дроссель должен работать.
Если у нас есть готовый дроссель, то тем самым мы знаем его геометрические и конструктивные размеры; к ним относится следующее:
Q — сечение железного сердечника, в кв. сантиметрах;
W — полное число витков обмотки;
d0 — диаметр обмоточного провода в миллиметрах;
q — сечение обмоточного провода в кв. миллиметрах;
lж — средняя длина пути, который проходит магнитный поток в железе, и
Iн — нормальная сила тока, при которой должен работать наш дроссель.
Самоиндукция дросселя будет зависеть от величины магнитного потока (считая все остальные величины, влияющие на изменение самоиндукции, как то: число витков, геометр. размеры и т. п., постоянными), или, вернее, от той части магнитного потока, который приходится на один квадратный сантиметр сечения железного сердечника, т. е. от магнитной индукции В. Придавая магнитной индукции В различные значения и создавая такие условия, в которых магнитная индукция достигла бы этой заданной величины, мы тем самым сможем изменять самоиндукцию дросселя в известных пределах.
Магнитный поток и, следовательно, магнитная индукция, зависят от силы тока, протекающего через обмотку дросселя и от так называемого «магнитного сопротивления», иными словами, от длины того пути как в железе, так и в воздухе, по которому должен пройти магнитный поток. Поэтому, подбирая соответствующим образом воздушный зазор, мы можем изменять магнитное сопротивление цепи и получать желаемую магнитную индукцию.
Выше уже указывалось, что работа дросселя будет протекать удовлетворительно лишь тогда, когда изменение силы тока будет вызывать пропорциональное изменение матнитного потока. Это условие ставит предел в выборе величины магнитной индукции. Поэтому для нормального железа ее не следует брать свыше 10000; наилучшие результаты получаются при В от 6000 до 8000.
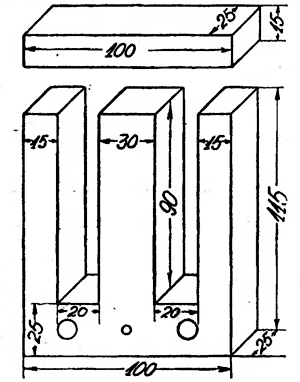
Для лучшего уяснения мы параллельно изложению способа подсчета самоиндукции дросселя и его воздушного зазора будем производить также и самый расчет. Пусть у нас имеется дроссель с Ш-образным сердечником. Общий вид сердечника и накладки показаны на рис. 1. Все размеры даны в миллиметрах.
Дроссель имеет обмотку из проволоки диаметром 0,25 мм в количестве 900 витков и предназначен для работы при силе тока 100 миллиампер.
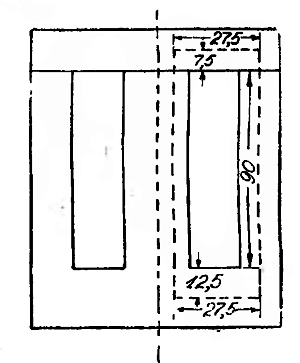
Ш-образный дроссель рассчитывается точно так же, как и П-образный, причем его можно рассматривать как два отдельных П-образных дросселя, имеющих каждый полное число витков, соединенных вместе. Катушка у такого дросселя надевается на средний стержень и магнитный поток, вызываемый этой катушкой, по выходе со среднего стержня раздваивается, и одна половина его идет через правый стержень, а другая — через левый. Для подсчета нужно знать лишь тот путь по железу, который проходится одной из половин магнитного потока. Из рис. 2 этот путь Iж нетрудно определить; он показан здесь пунктирной линией и на нем помечены размеры отдельных участков в миллиметрах.
Тогда:
| Iж = 90 + 12,5 + 27,5 + 12,5 + 90 + 7,5 + + 27,5 + 7,5 = 275 мм = 27,5 см. |
| Q = 3 × 2,5 = 7,5 кв. см. |
| d0 = 0,25 мм; q = | πd0 | = | 3,14 · 0,252 | ≈ 0,05 кв. мм. |
| 4 | 4 |
| W = 9000 витков; Iн = 0,1 амп. |
Для предварительного определения самоиндукции дросселя считаем, что магнитная индукция В равна 7000. Самоиндукция вычисляется по известной нам уже формуле, но решенной относительно L:
| L = | W · Q · B0 | · 10—8 генри ...... (1) |
| Iн |
Решаем эту формулу для нашего дросселя, подставляя в него известные нам величины:
| L0 = | 9000 · 7,5 · 7000 | · 10—8 = 47,25 генри. |
| 0,1 |
Если полученная самоиндукция нас не удовлетворяет, мы можем ее изменить до 20% в ту или другую сторону, причем для этого, как было сказано выше, должна быть изменена магнитная индукция.
Величина последней будет:
| В1 = | L · I0 | · 108 .......... (2) |
| W · Q |
где L — будет уже не найденная выше по формуле 1, а желаемая для нас самоиндукция.
Так, например, если дроссель для наших целей должен иметь самоиндукцию не 47,5, а лишь 40 генри, то
| В1 = | 40 · 0,1 | · 108 = 5926 гаусов. |
| 9000 · 7,5 |
Далее определяются те условия, при которых действительная магнитная индукция будет соответствовать вычисленной по формуле (2); иначе говоря, нам нужно подсчитать размер воздушного зазора.
Делается это тем же способом, который был приведен для расчета проектируемого дросселя.
Определяем полное число ампер-витков дросселя:
| (AW)π = Iн · W ....(3) |
что для нашего примера даст:
| AWπ = 0,1 · 9000 = 900 ампер-витков. |
Ампер-витки, расходуемые на путь в железе
| (AW)ж = (aw)ж · Iж. |
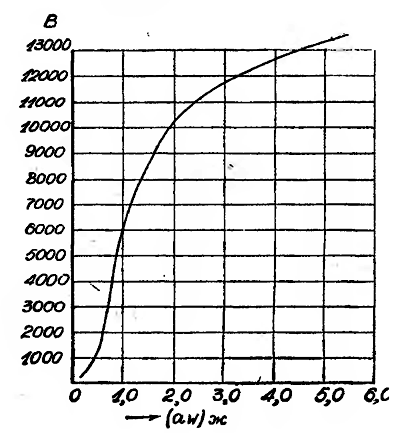
Величина (aw)ж берется из кривой, данной на рис. 3 или на приведенной в первой части таблицы.
Так, для В = 5926 число ампер-витков, расходуемых на 1 см пути в железе, будет по кривой приблизительно 0,96, и
| (AW)ж = 0,96 · 27,5 = 26,4 ампер-витка. |
На воздушный зазор приходится весь остаток ампер-витков, т. е.
| (AW)в = (AW)π — (AW)ж ........ (3) |
или (AW)в = 900 — 26,4 = 873,6 ампер-витка.
Общую величину воздушного зазора получим из формулы
| lв = | 0,4 π (AW)в | ............ (4) |
| B |
Для нашего дросселя имеем:
| lв = | 0,4 · 3,14 · 873,6 | = 0,185 см = 1,85 мм. |
| 5926 |
Тогда ширина щели будет 1,85 : 2 = 0,925 мм.
Для полноты расчета нам остается определить еще две величины. Одна из них — плотность тока, т. е. то число ампер, которое приходится на один квадратный миллиметр сечения обмоточного провода. Плотность тока должна заключаться в пределах обычно от 1 до 2 ампер на кв. мм. Если она меньше, то это доказывает, что сечение провода не достаточно хорошо используется и провод можно было взять более тонким. Наоборот, при плотности тока более 2 ампер на кв. мм возможно нагревание провода, что, конечно, не особенно желательно.
Плотность тока
| i = | Iн | ............ (5) |
| q |
для нашего случая
| i = | 0,1 | = 2 А/мм2, |
| 0,05 |
что вполне допустимо.
Последняя величина — это падение напряжения в дросселе. Оно не должно быть особенно велико, так как тем самым увеличиваются потери установки. При трелеграфной работе большая потеря напряжения в дросселе ухудшает тон передатчика, и он получается непостоянным.
Для определения падения напряжения надо сперва вычислить омическое сопротивление обмотки дросселя. Оно будет
| R = | W · I0 | ............ (6) |
| 57 · q |
где I0 — средняя длина одного витка обмотки в метрах, а q — сечение провода.
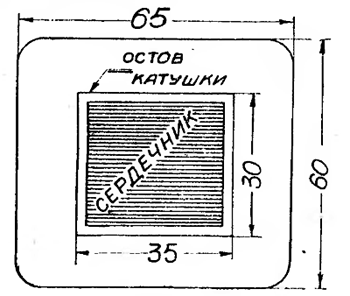
Среднюю длину одного витка получаем из рис. 4, где приведены размеры обмотки. Так как проволока намотана на картонный остов, то наиболее коротким витком будет, очевидно, тот, который прилегает к остову. Длина его будет 30 + 35 + 30 + 35 = 130 мм, или 0,13 м.
Наоборот, самым длинным витком будет виток, расположенный снаружи обмотки; его длина, как видно из рисунка, есть 65 + 60 + 65 + 60 = 250 мм или 0,25 м. Средняя же длина витка определится как полусумма обеих этих длин, а именно
| 0,13 + 0,25 | = 0,19 метра. |
| 2 |
Сопротивление всей катушки
| R = | 9000 · 0,19 | = 600 ом. |
| 57 · 0,05 |
Падение напряжения в ней выразится
| е = Iн · R ............(7) |
или
| e = 0,1 · 600 = 60 вольт, |
что надо принять во внимание при расчете выпрямительного устройства.