

Инж. А. Н. Попов.
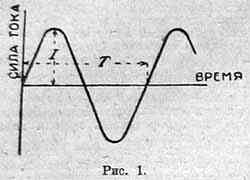
Мы знаем, что переменный ток изображается кривой, которая показана на рис. 1. Отрезок времени, обозначенный буквой Т, называется периодом тока. Волнообразная кривая такого вида, как показано на рис. 1, называется синусоидой. Она принадлежит к классу так называемых периодических кривых. Эти кривые обладают тем свойством, что, по прошествии определенного времени, — периода, — величина, которую они изображают, принимает те же значения, которые она имела, раньше.
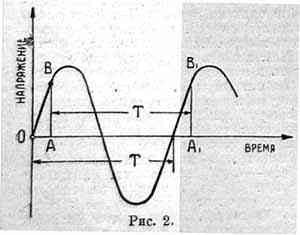
Чтобы уяснить себе это, обратимся к рис. 2. Пусть у нас имеется в какой-нибудь цепи напряжение частоты 50 периодов в секунду, изображаемое синусоидой. По прошествии времени 0А (например 1/300 секунды), мгновенное напряжение изобразится отрезком АВ (скажем 80 вольт). По прошествии периода, который в данном случае равен, 1/50 сек., напряжение изобразится отрезком А1В1. Закон периодичности заключается в том, что А1B1 равно АВ, т. е. напряжения для момента времени 1/300 сек. и (1/50 + 1/300) сек. равны по величине и по знаку: мы получим те же 80 вольт, которые будут действовать в том же направлении.
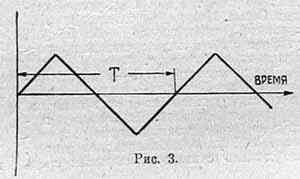
По внешнему виду периодические кривые легко отличить, так как они всегда имеют волнообразную форму. На рис. 3—7 показаны различные виды таких кривых.
Все то, что мы до сих пор говорили про переменный ток, относилось к току, который меняется по синусоиде. Все законы и расчеты относятся именно к такому виду переменного тока. В действительности, как в электротехнике, так в особенности в радиотехнике, приходится сплошь и рядом иметь дело с токами, которые меняются по кривым, весьма отличным от синусоиды. Примеров этому можно привести очень много. Здесь мы остановимся лишь на важнейших случаях.

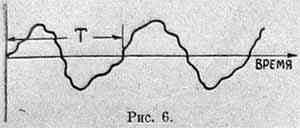
Прежде всего, кривую, отличную от синусоиды, дает человеческий голос. Как известно, и в обычном телефоне, и в радиотелефоне звук (речь, пение и т. п.) воздействуют на особый прибор, микрофон, который меняет ток в цепи, куда он включен, в такт с звуковыми колебаниями. Кривую тока, которая получается после микрофона, можно с помощью специальных приборов сфотографировать и по ней судить о виде звуковой кривой. Оказывается, что, если пропеть на определенной ноте какую-нибудь гласную, скажем «А», — то получается не синусоида, а очень сложная и причудливая периодическая кривая, похожая на кривую рис. 6.
Далее не синусоиду мы получим в любом выпрямителе и детекторе. Принцип действия этих приборов основан на том, что они обладают большой проводимостью в одном направлении и очень малой в другом. Благодаря этому, если подвести к ним синусоиду, то одна половина ее срежется и, после детектора или выпрямителя, мы получим половинки, «горбыли» от синусоиды, показанные на рис. 7. В частности: при схеме так называемого «однополупериодного» выпрямления, напряжение после выпрямителя будет как раз такое, как показано на рис. 7.
Упомянем еще две области, где могут получиться искаженные (не синусоидальные) напряжения и токи: это ламповые генераторы и цепи с железом. Заметим здесь же, что в радиотехнике больше всего приходится иметь дело с синусоидами, «подрезанными» сверху и снизу.
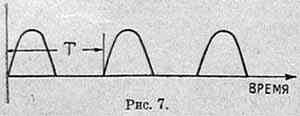
Разбор явлений в цепях с несинусоидальными напряжениями был бы очень труден, если бы не выручало одно замечательное свойство подобных кривых. Оказывается, что любую периодическую кривую можно разложить на ряд синусоид с периодами, уменьшающимися в целое число раз, или, что то же, с частотами, возрастающими в 2, 3, 4 и т. д. раз по отношению к основной. Поясним этот чрезвычайно важный закон, установленный французским ученым Фурье.

Обратимся к рис. 8. Кривая 1 представляет собою простую синусоиду с периодами Т1. Тонкая 2-я кривая тоже синусоида, но только с меньшим периодом. Пока кривая 1 проделывает полпериода (один горбыль), кривая 2 с периодами Т2 описывает уже полный период, т. е. Т2 в два раза меньше Т1, или частота второй кривой вдвое больше. Нетрудно видеть, что период Т3 третьей кривой равен 1/3 от Т1, т. е. частота третьей кривой втрое больше, чем первой. По отношению к первой «основной» кривой, кривые 2, 3 и т. д., частоты которых в 2, 3 и т.д. раза больше первой, называются второй, третьей и т. д. гармоническими. Часто их называют высшими гармоническими или просто «гармониками» 2).
Закон Фурье, таким образом, гласит следующее: если у над имеется сложная периодическая кривая с периодами Т, то всегда можно подобрать ряд кривых с периодами Т, Т/2, T/3, T/4 и т. д. с различными амплитудами таким образом, что, складывая вместе все эти кривые, мы в результате получим заданную кривую. Здесь необходимы некоторые замечания. Этот «подбор» отнюдь не представляет собой чего-либо гадательного. Существуют и математический, и целый ряд графических способов разложения произвольных кривых, причем все гармонические получаются вполне однозначно с своими амплитудами и взаимным расположением друг к дружке. Здесь мы, однако, пояснить этого не можем.
Далее нужно сказать, что это разложение дает нам заданную кривую приближенно. Чем больше гармоник мы возьмем, тем ближе будет их сумма к нашей кривой. Но так как все наши расчеты лишь приближенные, то ряда гармоник, скажем до 10, бывает вполне достаточно для изображения какой-нибудь кривой. При разложении обнаруживается ясное и с первого взгляда явление: чем больше наша кривая похожа на синусоиду, тем меньше нужно взять гармонических, чтобы достаточно хорошо ее изобразить; тем меньше также будут амплитуды гармоник.

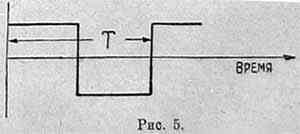
На рис. 9 показано разложение треугольника. Эта кривая, за исключением макушки, очень близка к синусоиде. Поэтому у нас большая основная сидусоида (1), а гармоники имеют маленькие амплитуды и число их не велико. На рисунке взяты 4 гармоники (1, 3, 5 и 7). Крестиками обозначены точки, которые получаются, если сложить эти 4 кривых. Мы видим, что всюду крестики ложатся на нашу кривую, и только у самой вершины треугольника точка опустилась ниже, чем следует. Для кривых, более отличных от синусоиды, приходится брать большее количество гармоник. Особенно неудобна в этом отношении прямоугольная кривая (рис. 5).
Значение этих разложении ясно само собой. Эдс, обладающую сложной кривой, мы можем заменить рядом генераторов переменного тока с различными частотами, и рассматривать явления для каждой гармоники в отдельности.
Теперь возникает вопрос: являются ли эти гармоники только хорошим приемом для того, чтобы упростить решение задач, или мы можем их ощущать в действительной обстановке?
Оказывается, что можем. С одним из самых неприятных проявлений гармоник мы сталкиваемся, когда передатчик (напр. радиотелефонный) дает не чистую синусоиду. Предположим, что основная частота передатчика соответствует длине волны в 1 400 метров. Тогда его вторая гармоника дает волну в 700 метров. Если мы слушаем станцию на волне в 700 метров, то (при достаточной силе) вторая гармоника первого передатчика будет влезать непрошенной частотой в наш приемник и искажать всю передачу.
Из предыдущих статей мы знаем, что индуктивное сопротивление цепи тем больше, а емкостное тем меньше, чем больше частота тока. Отсюда следует, что индуктивное сопротивление для 2, 3 и т.д. гармоник, будет в два, три и т. д. раза больше, чем для основной. Емкостное же сопротивление будет в 2, 3 и т.д. раза меньше. На этом принципе основаны приспособления, служащие для «отсеивания» нежелательных гармоник, так называемые фильтры.

Так, после выпрямления переменного осветительного тока, получается ток постоянный и ряд гармоник от 50 периодов, которые дают неприятное гудение в приемнике, если выпрямленный ток служит для питания последнего. Чтобы отсеять гармоники, применяют фильтр, показанный на рис. 10. Катушки самоиндукции обладают большим индуктивным сопротивлением и малым омическим. Поэтому, постоянный ток свободно проходит через них, а гармоники задерживаются. Вместе с тем, конденсаторы, включенные между проводами, дают удобный «сток» для переменных токов, не пропуская при этом постоянного. В результате, после фильтра мы получаем сглаженный постоянный ток, в значительной мере очищенный от гармоник.
1) См. "Радио Всем" № 3.
2) На рис. 8 кривые для ясности имеют разные амплитуды. Понятно, это не меняет дела.