

Для расчета катушек существует достаточно большое количество формул. Мы здесь приведем только наиболее простые, дающие в то же время достаточно точные для любительской практики результаты.
Однослойные цилиндрические катушки подсчитываются по формуле:
| L = 9,8D2n2lk |
В этой формуле приняты следующие обозначения:
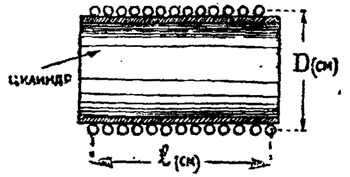
D — диаметр катушки в см (см. рис. 3),
n — число витков на 1 см длины катушки. Для получения n нужно полное число витков N разделить на длину намотки l, т. е.:
| n = | N | ||
| l |
l — длина намотки катушки в см.
L — самоиндукция катушки в см.
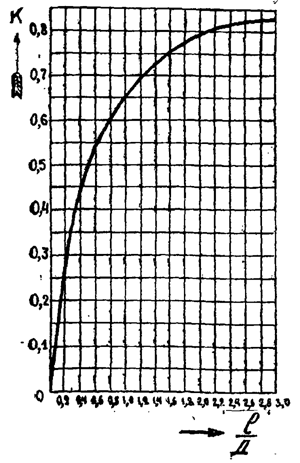
K — коэффициент, зависящий от отношения l/D (дан графически на кривой рис. 4).
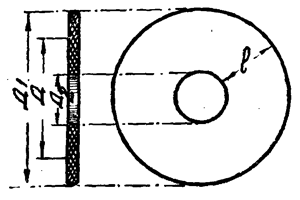
По этой же формуле можно определять самоиндукцию плоских спиральных катушек (рис. 5), только под D следует понимать «средний» диаметр, т. е.
| D = | D1 + D2 |
| 2 |
а l — не длина, а ширина намотки (см. рис. 5).
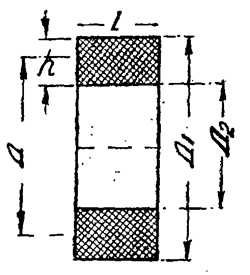
Самоиндукцию сотовых катушек можно приближенно подсчитать по формуле:
| L = 0,2714 | l2 |
| h |
где L — самоиндукция катушки в см,
l — длина намотанной проволоки в см.
h — толщина катушки в см (cм. рис. 6).
Проще всего самоиндукцию цилиндрических и сотовых катушек подсчитать по номограмме Бронштейна и Менщикова, данной на рис. 7.
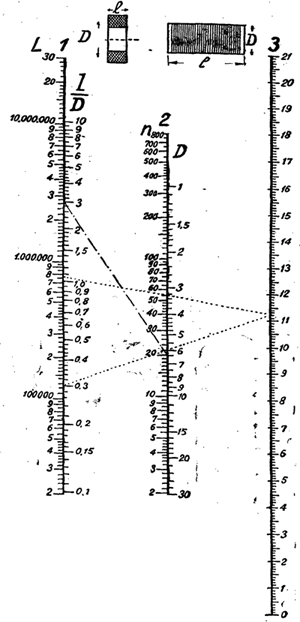
Способ применения ее следующий. Прежде всего определяется отношение l/D и n путем обычных вычислений. После этого соединяют, как уже было описано выше, линейкой точку l/D на шкале № 1 и точку D на шкале № 2. Полученную на вспомогательной шкале № 3 точку соединяют линейкой с точкой n на шкале № 2; пересечение линейки со шкалой № 1 дает точку, соответствующую искомой самоиндукции. На номограмме дано пунктиром определение самоиндукции сотовой катушки при
l = 1,8 см, D = 6 см, N = 100, l/D = 1,8/6,0 = 0,3; n = N/l = 100/1,8 = 55.
Аналогичным же путем определяется самоиндукция цилиндрических катушек.
В таблице III даны числовые значения для стандартных сотовых катушек, т. е. катушек, имеющих внутренний диаметр = 5 см, и ширину = 2,5 см.
| Число витков |
Диаметр проволоки с изоляцией в мм. |
Самоиндукция в cм. |
Сопротивле- ние в омах. |
Наружный диаметр ка- тушки в см. |
Длины волн при конденсаторе макс. емкостью в 1000 см. |
Длина прово- локи в метрах |
| 25 | 0,56 | 52000 | 0,5 | 5,5 | 180—430 | 4 |
| 36 | 88000 | 0,75 | 5,6 | 200—560 | 6 | |
| 50 | 106000 | 1,25 | 5,7 | 250—613 | 9 | |
| 75 | 293000 | 1,5 | 5,9 | 400—1020 | 14 | |
| 100 | 543000 | 1,75 | 6,2 | 500—1310 | 20 | |
| 150 | 1140000 | 2,5 | 6,6 | 700—2010 | 30 | |
| 200 | 2190000 | 4,25 | 6,9 | 1000—2790 | 42 | |
| 250 | 0,5 | 3676000 | 5,5 | 7,2 | 1300—3610 | 50 |
| 300 | 5170000 | 6,0 | 7,6 | 1600—4260 | 63 | |
| 400 | 8750000 | 9,0 | 8,0 | 2000—5575 | 84 | |
| 500 | 14350000 | 11,0 | 9,2 | 2500—7150 | 115 | |
| 600 | 19660000 | 12,5 | 7,8 | 3200—8350 | 122 | |
| 760 | 0,36 | 31700000 | 20,5 | 8,2 | 4000—10600 | 160 |
| 1000 | 59260000 | 36,0 | 9,3 | 6000—14500 | 225 |
Емкость многопластинчатого плоского конденсатора определяется по формуле:
| C = | εS(n—1) | ||
| 12,5d |
В этой формуле приняты следующие обозначения:
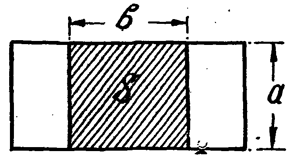
S — площадь одной обкладки в кв. см. S = a × b (рис. 9 и 10).
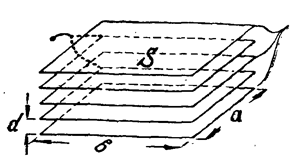
При определении площади обкладок следует за S принимать только ту часть площади, которая перекрывается обеими обкладками.
n — общее число обкладок,
d — расстояние между обкладками (толщина диэлектрика) в см.
ε — диэлектрическая постоянная, разная для различных диэлектриков. Значения ε приведены в таблице IV.
| Диэлектрик | ε = | Диэлектрик | ε = |
| Пустота........ | 1 | Бумага (сухая)... | 1,8—2,6 |
| Воздух........ | 1,0006 | Каучук........ | 2,0—3,5 |
| Керосин........ | 2 | Парафин........ | 1,8—2,3 |
| Эбонит........ | 2—3 | Сера........ | 3,6—4,8 |
| Маслян. бумага. | 3 | Целлюлоза........ | 4 |
| Шеллак........ | 3,0—3,8 | Сургуч........ | 4 |
| Стекло........ | 5—10 | Вода (химич. чистая)........ |
31 |
| Слюда........ | 5—8 |
С — емкость конденсатора в см.
Так как расчет емкости по этой формуле связан с некоторыми затруднениями, то мы приводим таблицу V, где даны емкости при различных толщинах диэлектрика, разном числе обкладок и при слюдяном и бумажном (пропарафинированном) диэлектрике, причем площадь обкладки принята равной 1 кв. см. При определении емкости какого-нибудь конденсатора следует при данных d и n просто помножить цифру, полученную из таблицы, на величину площади обкладки, взятую в кв. сантиметрах.
| d (см) | Число пластин | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 0,005 | 31,9 | 63,8 | 95,7 | 127 | 159 | 191 | 223 | 255 | 287 | 319 | 351 | Парафин ε = 2 |
| 0,01 | 15,9 | 31,9 | 47,8 | 63,7 | 79,6 | 95,5 | 111 | 127 | 143 | 159 | 179 | |
| 0,03 | 5,3 | 10,6 | 15,9 | 21,2 | 26,5 | 31,9 | 37,2 | 42,5 | 47,8 | 53,2 | 58,5 | |
| 0,05 | 3,2 | 6,4 | 9,5 | 12,7 | 15,9 | 19,1 | 22,3 | 25,5 | 28,7 | 31,9 | 35,1 | |
| 0,08 | 1,99 | 3,98 | 5,96 | 7,95 | 9,95 | 11,9 | 13,9 | 15,9 | 17,9 | 19,9 | 21,8 | |
| 0,1 | 1,59 | 3,19 | 4,78 | 6,37 | 7,96 | 9,55 | 11,1 | 12,7 | 14,3 | 15,9 | 17,5 | |
| 0,005 | 95,6 | 191 | 287 | 381 | 477 | 572 | 669 | 765 | 860 | 956 | 1050 | Слюда ε = 6 |
| 0,01 | 47,7 | 95,6 | 143 | 191 | 239 | 286 | 333 | 381 | 428 | 476 | 524 | |
| 0,03 | 15,9 | 31,8 | 47,7 | 63,5 | 79,4 | 95,5 | 111 | 127 | 143 | 159 | 175 | |
| 0,05 | 9,6 | 19,2 | 28,7 | 38,1 | 47,7 | 57,2 | 66,9 | 76,5 | 86,0 | 95,6 | 105 | |
| 0,08 | 5,9 | 11,9 | 17,9 | 23,9 | 29,9 | 35,7 | 41,7 | 47,7 | 53,7 | 59,7 | 65,4 | |
| 0,1 | 4,7 | 9,5 | 14,3 | 19,1 | 23,9 | 28,6 | 33,3 | 38,1 | 42,8 | 47,6 | 52,4 | |
При параллельном соединении двух конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов:
| C = C1 + C2 |
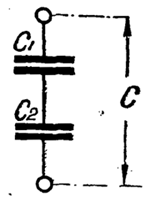
При последовательном соединении конденсаторов (рис. 11) общая емкость определяется формулой:
| C = | C1C2 | ||
| C1 + C2 |
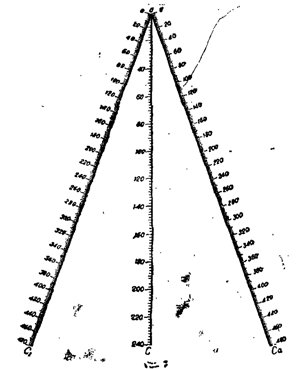
На рис. 12 дана номограмма для определения емкости двух последовательно включенных конденсаторов. На наклонных столбцах даны емкости С1 и С2, на среднем столбце дана общая емкость С. Нужная общая емкость получится, если соединить линейкой соответствующие емкости на крайних столбцах.
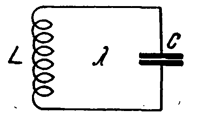
Соединение катушки самоиндукции с конденсатором так, как показано на рис. 13, образует колебательный контур.
Частота колебаний, как известно, может быть заменена понятием длины волны.
Длина волны колебательного контура определяется формулой Томсона:
| λ = | 2Π | √ LC | ||
| 100 |
где λ — длина волны в метрах,
L и С — самоиндукция и емкость контура в см.
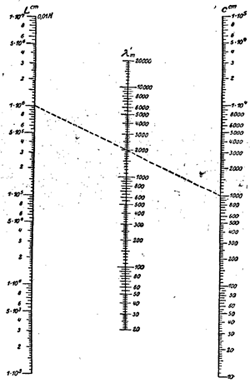
Расчет длины волны по формуле Томсона может быть заменен расчетом по номограмме рис. 14. Здесь на боковых столбцах отложены величины L и С в сантиметрах, а на среднем столбце длина волны в метрах. Зная две из приведенных величин, можно очень легко с помощью линейки, как это уже было описано выше, определить третью величину.

1) Начало см. «Р. В.» № 14. (стр. 389.)