

Б. П. Асеев.
В настоящей статье мы остановимся на рассмотрении и объяснении результатов последнего наблюдения с экспериментальной схемой лампового генератора.
Производя последний опыт, мы заметили, что индикаторная лампочка, или тепловой измерительный прибор дает наибольшее свечение или отклонение при определенном положении указателя переменного конденсатора, иначе говоря, при определенной емкости в колебательном контуре.
Чтобы разобраться в этом, следует вначале остановиться на вопросе, что происходит в колебательном контуре при изменении емкости его конденсатора? Влияние изменения емкости конденсатора будем рассматривать с точки зрения изменения величины сопротивления колебательного контура.

Что же следует подразумевать под сопротивлением контура? Здесь надо ввести понятие о сопротивлении контура постоянному и переменному току. Если к зажимам контура (рис. 1) приключить источник постоянного тока (батарею), то возникший ток, дойдя до точки разветвления А (рис. 1), пройдет исключительно через ветвь с катушкой L, так как конденсатор С представляет для постоянного тока бесконечно большое сопротивление (разрыв цепи). Катушка L является для постоянного тока весьма малым сопротивлением, которое и следует рассматривать как сопротивление контура постоянному току. Поскольку это сопротивление очень мало, то им, обычно, пренебрегают и считают, что для постоянного тока контур LC не представляет сопротивления.
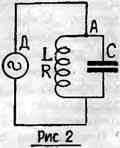
Иная картина получается при питании контура LC от источника переменного тока (динамо-машины переменного тока Д — рис. 2). Здесь переменный ток, дойдя до точки разветвления А, пойдет в через ветвь с емкостью и через ветвь с самоиндукцией. Как емкость, так и самоиндукция представляют собой для переменного тока определенные сопротивления; эти сопротивления, будучи соединены параллельно, дают общее сопротивление контура, которое, как учит теория, тем больше, чем больше коэффициент самоиндукции катушки L и чем меньше емкость конденсатора С и омическое сопротивление R (рис. 2); под омическим сопротивлением R подразумевают сопротивление катушки L и подводящих проводников.
Сопротивление контура переменному току =

Написанную формулу отметим номером 1.
Надо заметить, что по формуле №1 сопротивление контура может быть вычислено лишь при условии резонанса между частотой контура LC и частотой машины Д (рис. 2). В ламповом генераторе всегда имеется резонанс между частотой контура и частотой питающего его тока; указанное выше заключение сделано исключительно для предупреждения ошибки, которая будет получена при подсчете по формуле №1 сопротивления контура для любых условий его работы.
Из изложенного следует, что при изменении емкости переменного конденсатора контура, изменяется сопротивление последнего для переменного тока.
У читателя, естественно, может возникнуть вопрос: для чего мы рассматриваем сопротивление контура переменному току, когда в цепи анода лампы, где работает колебательный контур, циркулирует постоянный ток.
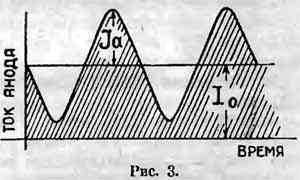
Выяснению вопроса о наличии переменного тока в анодной цепи лампы нам поможет рис. 3, который является повторением части рис. 3, помещенного в № 3 «Радио Всем». Рассматривая рис. 3, убеждаемся, что в цепи анода лампы (при колебаниях) протекает постоянный по направлению, но переменный по силе ток, который принято называть пульсирующим (заштрихованная площадь на рис. 3). Нетрудно видеть, что этот пульсирующий ток можно представить состоящим из двух слагаемых постоянного тока I0 (рис. 3) и переменного Ja 1); отдельно эти слагаемые изображены на рис. 4. В справедливости нашего разложения можно убедиться обратным действием — сложением токов I0 и Ja; для выполнения этого действия наложим линию СД (рис. 4) на линию АВ и получим суммарную кривую, в точности соответствующую рис. 3.

Таким образом в анодной цепи лампы имеются как бы два тока — постоянный I0 и переменный Ja. Для постоянного тока I0 контур LC не представляет практически никакого сопротивления; что же касается переменного тока Ja, то ему контур LC оказывает значительное сопротивление, величина которого определяется по формуле №1.
Основная задача генераторной схемы — создать возможно большую колебательную мощность в контуре LC. Для выполнения этой задачи, как следует из теории, сопротивление контура переменному току должно иметь вполне определенную величину.
Величина сопротивления контура, при которой в нем создаются наиболее мощные колебания, так называемое «наивыгоднейшее сопротивление», зависит от напряжения анодной батареи и от тока насыщения лампы. Приближенно «наивыгоднейшее сопротивление» может быть определено по следующей формуле:
наивыгоднейшее сопротивление =
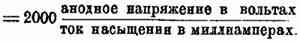
Эту формулу обозначим №2.
Например, если напряжение анодной батареи равно 120 вольт, а ток насыщения — 12 миллиампер, то по формуле №2 наибольшая мощность в контуре будет получена в том случае, когда его сопротивление переменному току будет равно:

Допустим, что в цепи анода этой лампы находится колебательный контур, имеющий следующие данные: коеффициент самоиндукции катушки — 25 000 сантиметров; емкость конденсатора — 180 см и омическое сопротивление — 5 ом.
Пользование формулой №1, в случае выражения величин емкости и самоиндукции в сантиметрах, возможно при условии увеличения полученных результатов в 900 раз, т. е.
сопротивление контура =
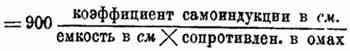
Эту формулу обозначим №3.
Подставляя в формулу №3 приведенные выше цифры, получаем:
сопротивление контура =

Результаты нашего вычисления показывают, что в данном случае сопротивление контура переменному току имеет величину большую, чем это необходимо (сопротивление контура = 25 000 ом, а величина, необходимая для получения наибольшей мощности, равна 20 000 ом).
Проделаем еще одно вычисление: положим, что самоиндукция катушки и омическое сопротивление контура остались без изменения, а емкость переменного конденсатора увеличена до 225 сантиметров.
Подставляя эти цифры в формулу №3, получим сопротивление того же контура при емкости конденсатора 225 см равным
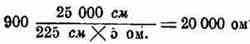
Таким образом, при емкости переменного конденсатора 225 см колебательный контур имеет необходимую нам величину сопротивления — 20 000 ом.
Наконец, увеличим емкость конденсатора до 300 см и определим для этого случая сопротивление контура:
сопротивление контура =

В данном случае сопротивление контура меньше, чем это необходимо.
Итак: 1) при данном анодном напряжении и токе насыщения сопротивление контура для получения в нем наибольшей мощности должно иметь вполне определенную «наивыгоднейшую» величину (формула №2); 2) изменяя емкость переменного конденсатора, мы тем самым меняем сопротивление контура и при некоторой величине этой емкости (в нашем численном примере — 225 см) сопротивление контура как раз равно «наивыгоднейшей» его величине; 3) при равенстве сопротивления контура «наивыгоднейшему» сопротивлению в контуре создается наибольшая мощность, и индикаторная лампочка дает максимальное свечение.
В рассмотренном нами примере происходила подгонка сопротивления контура к наивыгоднейшей величине сопротивления (изменением емкости переменного конденсатора). Вполне возможно и обратное явление: подгонка «наивыгоднейшего» сопротивления к сопротивлению контура, так сказать, подгонка лампы под данный колебательный контур.
Возьмем третий случай численного примера: при емкости переменного конденсатора 300 см сопротивление контура равно 15 000 ом., а наивыгоднейшее сопротивление, которое было нами вычислено по формуле №2, равно 20 000 омов.
Для устранения этого недостатка существуют способы, позволяющие проделывать подгонку контура к наивыгоднейшей величине сопротивления без изменения длины волны контура.
Этот метод будет разобран в следующей статье.
1) См. о разложении кривых статью инж. Попова в № 3 "Р. В." за 1928 г.2)
2) В статье Попова в №3 "Р. В." описывается, скорее сопротивление конденсатора и индуктивности постоянному и переменному току. Разложение кривых переменного тока на гармоники описывается в статье Попова в № 4 "Р. В." за 1928 г. (примечание составителя).